Investigation on Spectral properties of 3-Chloro-3'-Methoxystilbene for Anticancer Drugs Application: Using Density Functional Theory

A. Prakasam^b

^aDepartment of Physics, Periyar University, Salem - 636 011, India.

^bDepartment of Physics, Thiruvalluvar Government arts college, Rasipuram, Namakkal – 637 401, India

Harold Hilarion Fokoue(hfokoue@gmail.com)

Nursel Acar(nursel.acar@ege.edu.tr)

Mahnaz Mohammadi(mohammadi.m@qut.ac.ir)

Bo Shang(bshang@cqu.edu.cn)

A. Prakasam, T.Saravana Kumaran, Investigation on Spectral properties of 3-Chloro-3'-Methoxystilbene for Anticancer Drugs Application: Using Density Functional Theory(2019)Journal of Computational Chemistry & Molecular Modeling 3(2)p:294-312

The ground state optimized structure and spectroscopic analysis of 3-chloro-3'-methoxystilbene (3C3'MS) were studied experimentally by FT-IR techniques and computationally by the first principle density functional theory (DFT) and Hartree-Fock (HF) method with 6-311++G (d, p) level of theory. The computational vibrational frequencies have been assigned and they agreed satisfactorily with experimental FT-IR and FT-Raman spectra. The computed maximum wavelength of absorption of 3C3'MS are calculated in different solvents (Acetonitrile, Methanol and Ethanol) by TD-DFT method. The experimental available ¹H and ¹³C nuclear magnetic resonance chemical shifts calculations have been calculated by using the Gauge independent atomic orbital (GIAO) method and compared with the computational studies. The NBO atomic charges analysis in conjunction with spectral data recognized the occurrence of intra-molecular interactions such as hyperconjugative, mesomeric and steric effects in 3C3'MS. Electronic distribution and Frontier molecular orbital energy values of 3C3'MS are discussed in terms of intra-molecular interactions. Computed values of Mulliken charges, Quantum Chemical descriptors and thermodynamic properties of 3C3'MS along with molecular electrostatic potential (MEP) are reported. Moreover, the estimation of the molecule confirms the biological behavior.

Keywords: FT-IR, FT-Raman, NMR spectra, NBO, NLO and NPA analysis, Thermodynamic properties, MEP analysis.

Stilbene and its derivatives are one of the most thoroughly studied compounds from the standpoint of mechanistic and preparative photochemistry [1-5]. The importance of the ring closure reaction channel in cis and trans-stilbene was recognized early [6] and most in recent time’s stilbene has become a prototype for ultrafast studies of photoisomerization [7-10]. The importance of stilbene photochemical analogous studies has been performed for only a limited range of stilbene and its derivatives. Our final goal is to obtain a clearer picture of the effect of different solvents and substituents on photochemical processes for cis and trans-stilbene derivatives. In these derivatives are important oligomeric compounds with a broad range of biological action, including hormonal, hypocholsterolemic, Sympathomimetic, antifungal, antiallergic, Human hemoglobin, antibacterial, antimalarial, Human serum albumin and anticancer activity. 3-chloro-3'-methoxystilbene are very important bioactive molecule [11-14]. The most famous stilbene derivatives, which was used medically for prostate and breast cancer, and to prevent threatened abortions [15-18]. Seigo sanoh et al. reported the trans-stilbene is metabolically activated to estrogenic compounds by liver microsomal enzyme molecular system. The physical requirement for estrogenic activity of different stilbene derivatives (Cis and Trans) including proestrogens [19]. Kyosuke Tsumura et al. reported DFT and TD-DFT, together with the analytical calculation of numerical and gradients calculation of the Hessian matrix has been applied to calculate the FT-IR, FT-Raman and fluorescence excitation spectrum of trans-stilbene (tSB) in the lowest excited singlet (S1) state [20]. The Excited-state reduction of cis-stilbene and trans-stilbene is outlined with femtosecond computed FT-Raman spectroscopy, using S_n→S₁ resonance conditions. For isomers, decay in FT-Raman shift, intensity of spectral positions and mind broadening of the bands specify IVR. In n-hexane this process effectively takes 0.5-0.7 ps [21]. Rajat K. Chaudhuri et al. reported Molecular  geometries are calculated for the ground state and excited states of 4a,4b-dihydrophenanthrene (DHP), cis-stilbene, and trans-stilbene from calculations accomplished with the developed fundamental orbital, complete active space configuration intermolecular interaction (IVO-CASCI) method. The calculations indicate that a nonplanar conformer of tSB is the most stable between the photoisomers [22].The photoisomerization dynamics of tSB have been well studied in the lowest excited state, but much less is known about the performance following excitation to higher excited states. This contribution reports a combined study of the spectroscopy and dynamics of two-photon available states above S1. Two-photon absorption (2PA) measurements using a broadband pump−probe technique reveal distinct bands near 5.1 and 6.4 eV are reported by Amanda L. Houk et al [23].

Nowadays, Modern vibrational spectroscopy has become a very popular analytical technique for solving many chemical problems. This is especially true of studies using Raman spectroscopy is a powerful technique, which gives information about the vibrations modes of the atoms and molecular structure, specific information on various chemical composition and Fourier transform infrared spectroscopy (FT-IR) is as an analytical method to identification of the functional groups, the degree of conjugation and interaction with drugs. The problem of signal vibrations however, as well as understanding the relationship between the observed vibration spectra and molecule structure, and chemical reactivity can be difficult. Even identification of important vibrational modes often generates controversy [24].  Recently, computational technique and DFT is an advance quantum chemical approach that plays an important role in the understanding of molecular system, vibrational spectrum and of the various properties of biological activity [25-28]. In particular for polyatomic molecules the quantum chemical method lead to the calculation of the  more perfect molecular system and vibrational Spectrum (Infrared and Raman spectroscopies) than the conventional ab initio RHF and MP2 method [24] and the three-parameter B3LYP density functional, which includes Becke’s gradient exchange correction [29] and the Lee-Yang-Parr correlation functional [30].

In previous work, we wish to report the experimental and theoretical investigation of vibrational spectral analysis and ground state geometric structure of this bioactive 3-Chloro-3'-Methoxystilbene molecule and their results have been discussed. Moreover, the calculated vibrational wavenumber of potential energy distribution (PED) was assigned and Molecular Electrostatic Potential (MEP) map of title compound has been reported. The HOMO-LUMO energy gap to supports to pharmacological active property and Natural bond orbital (NBO) charge analysis has been performed to investigate charge transfer interactions and the hydrogen bonding within the molecule. The electronegativity, chemical hardness and softness values were also considered by utilizing frontier molecular orbital energy gaps of title compound.

2.1. Experimental Details

This chemical with a purity of 99% is purchased form Alfa Aesar chemical suppliers (India) and were used as received. FT-IR measurements were performed using Mattson 1000 FT-IR spectrometer in the 4000 and 400 cm^-1 region. The FT-Raman spectrum of 3C3'MS  was recorded between the region 4000 and 50 cm^-1 using a Bruker FRA 106/S FT-Raman instrument using 1064 nm excitation from an Nd: YAG laser. The detector used was a liquid nitrogen cooled Ge detector. ¹H NMR and ¹³C NMR spectrum was recorded at 400 MHZ on BRUKER AV-III 400 MHZ instruments.

2.2. Computational details

The theoretical calculations were performed using the Gaussian 09 program package [31]. The optimized geometries were obtained employing DFT and HF [32, 33] functional in conjunction with 6-311++G (d, p) basis set. Subsequently, the vibrational IR and Raman spectra were calculated at harmonic approximation. All the calculated computed harmonic frequencies were real, which confirm that the optimized structures correspond to minimum energies. The internal coordinates of the molecule were converted to the local symmetry coordinates. The distributions of assignment of the computed wavenumbers have been aided by means of MOLVIB-7.0 program [34, 35]. The Cartesian representation of the force constants were transferred to a non-redundant set of symmetry coordinates, internal coordinate system recommended by Pulay et al. [36] is used for the assignment of vibrational modes. All the molecular structures are pictured using software Gauss-view [37]. ¹H and ¹³C NMR isotropic shielding were calculated by GIAO method using optimized parameters obtained from DFT/6-311++G (d, p) method. The electronic properties such as oscillator strengths of electronic singlet-singlet transitions, absorption wavelengths and calculate energies were determined by TD-DFT method and Hence, the HOMO and LUMO energies and chemical hardness, softness, electrophilicity index and electronegativity were assumed from electron affinity and ionization potential have also been evaluated in the present study.

4.1 Molecular Geometry

The most optimized geometrical parameters such as, bond lengths, bond angles and dihedral angles of title compound calculated at initio DFT and HF methods with 6-311++G(d,p) level of theory and optimized structure of the host molecule along with numbering scheme in Fig. 1. The calculated bond lengths between C12-C2, C5-Cl17 in DFT and HF methods are found to be 1.3514, 1.3315 Å and 1.8309, 1.8117 Å respectively. The bond angle between C5-C4-20 in HF and DFT are 120.0677 and 119.6667^o respectively in Fig. 2b.The dihedral angle between C8-C3-C4-H20 in HF and DFT are 180.001^o and 179.9987^o respectively. The Computed geometrical parameters can be used to determine the other parameters of 3C3'MS. The bond lengths, bond angles and dihedral angles were referred from [38]. Fig.2. Graphical representation of correlation coefficient and linear relationships of between the DFT and HF bond lengths, bond lengths and dihedral angles were determined for 6-311++G(d,p) basis set.

The optimized bond lengths of C-H in methyl ring in calculated range from 1.0893, 1.0965, 1.0965 Å and 1.0762, 1.0823, 1.0823 Å for 3C3'MS. The C-H bond angles are found 109.7164, 109.6621, 109.7152 and 109.6616, 109.5451, 109.7381 Å for 3C3'MS respectively, from DFT and HF/6-311++G (d, p) methods, which are in good agreement with calculated values for C-H bond lengths and bond angles of methyl ring.

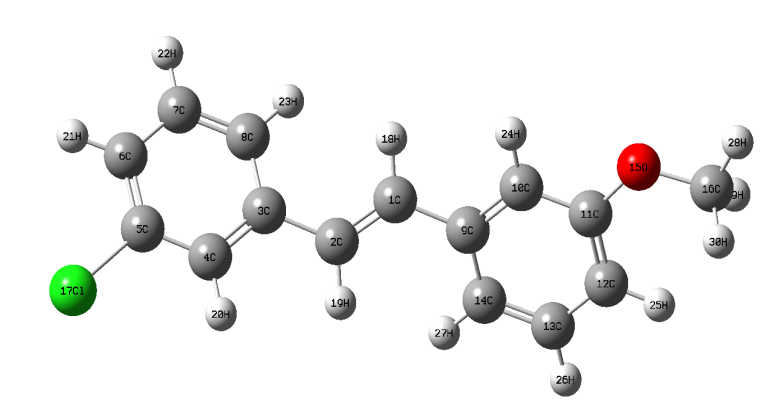
Fig. 1   Optimized geometrical structure

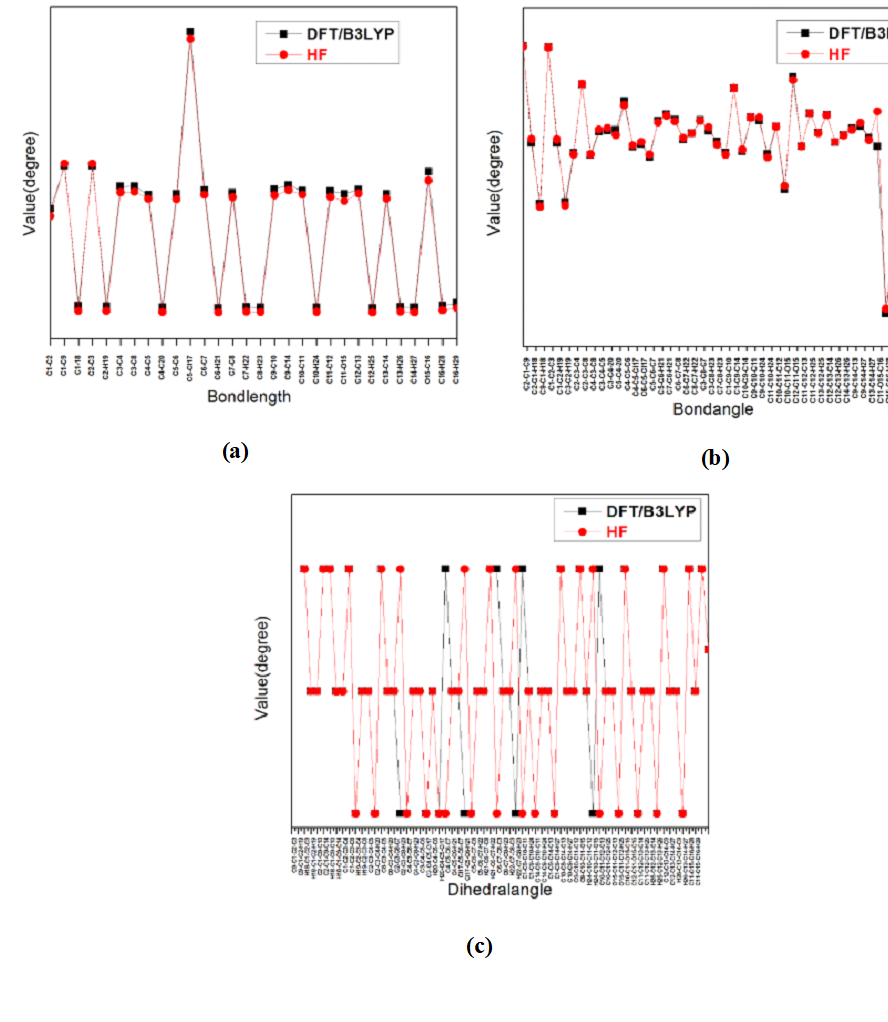
Fig. 2   Bond lengths, bond angles and dihedral angles differences between DFT and HF approaches

4.2 HOMO-LUMO energy gap

Frontier molecular orbitals (FMOs) play a major role in the kinetic stability or molecular chemical reactivity and the interactions between atoms. They are measured to be effective in determining the characteristics of the molecule such as pharmaceutical and biological activities. The organic molecule containing conjugated π electrons characterized by a small HOMO-LUMO separation energy, which is the result of a significant degree of Intramolecular change transfer (ICT) from the end-capping electron donor groups to the efficient electron acceptor groups through conjugated path [39]. The calculated HOMO-LUMO energy gap of the title molecule is -4.17 eV at the B3LYP level, respectively. The Large energy gap is basically a significance of the large stabilization of the LUMO due to the strong electron−accepting ability of the electron−acceptor group. The graphical diagram of HOMO and LUMO orbitals and their respective positive and negative regions are shown in Fig. 3. Such a plot suggests that in the HOMO → LUMO excitation the benzene ring π electrons are transferred to chloride group. The chemical reactivity of organic molecules such as chemical hardness and softness can be calculated from HOMO and LUMO energy gap values. The atomic π-orbital’s point towards each other and an increase in π-character points the fact that σ-bonds are stronger as showed by natural bond analysis. A highly delocalized LUMO indicates that the electrons can more readily move around the molecule from HOMO-LUMO and hence an improved ICT [40] shown in Table 1. The HOMO electrons are mostly localized on the methyl group attached to the benzene ring while LUMO is mainly delocalized on the benzene ring indicating the presence of favorable atomic center within 3C3'MS for possible nucleophile attacks(hydrogen bond acceptor)  revealing its bioactivity. Both the HOMO and LUMO are mainly localized around the two benzene rings which show that they are π type orbitals. There are lots of applications available for the use of HOMO and LUMO energy gap as a computational calculation.

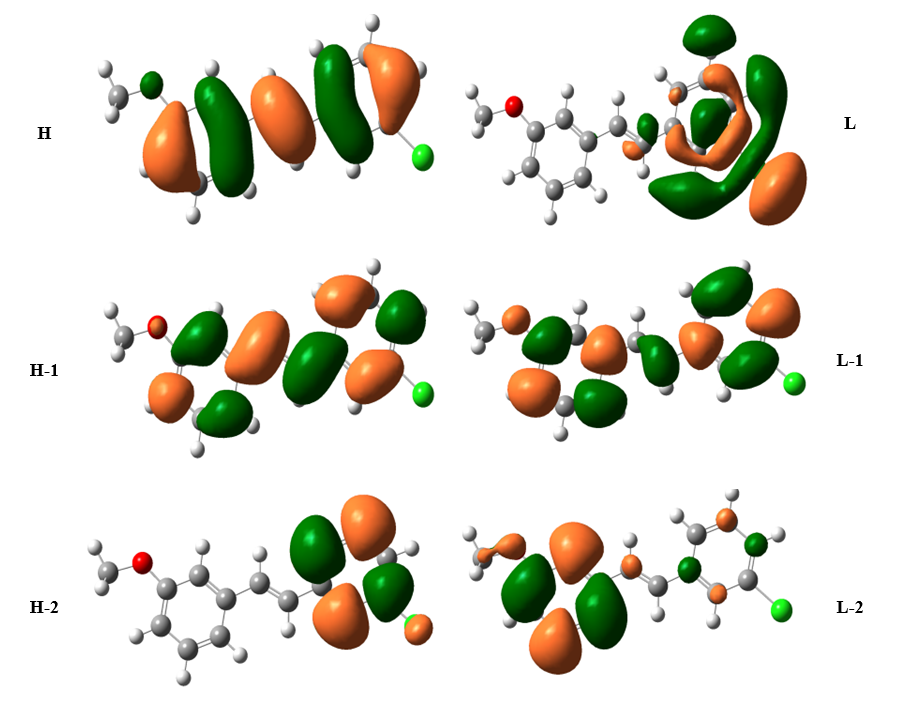
Fig. 3 Schematic view of the important Molecular Orbitals of TD-DFT/6-311++G (d, p) method.

Table 1. Molecular Properties end energy gap (eV) between molecular orbitals involved in electronic transitions of 3C3'MS.

Table 2. Definition of internal coordinates of 3C3'MS.

4.3 Vibrational analysis

The vibrational spectral analysis is to end vibrational frequencies connected with specific molecular structures of calculated title molecule. The normal vibrations are distributed as 56A'+31A'' considering C_s symmetry. All the 87 normal modes of vibrations are active in both IR and Raman. Vibrational wavenumber was calculated using the DFT and HF methods with the single split valence basis set 6-311++G (d, p). Table 3 the vibrational assignments in the present study are based on the scaled wavenumbers DFT and HF/6-311++G (d, p) vibrational frequencies, Reduced Mass, Raman activity, IR intensities, Depolarization Ratio, Force Constants and fundamental modes descriptions (characterized by PED) of the title compound. The comparison between the observed frequencies and the computational FT-IR and Raman spectra support each other. Including of electron correlation in computational theory to a certain extend makes the frequency values smaller in comparison with the HF frequency data. All frequency modes are active both in IR and Raman Spectra. For this purpose, the full set of 87 normal internal coordinates and description of vibrational assignments of fundamental modes can be given by means of normal coordinates have been reported in Table 2. The calculated and experimental of FT-IR [41], FT-Raman spectra are shown in Figs. 4 and 5.

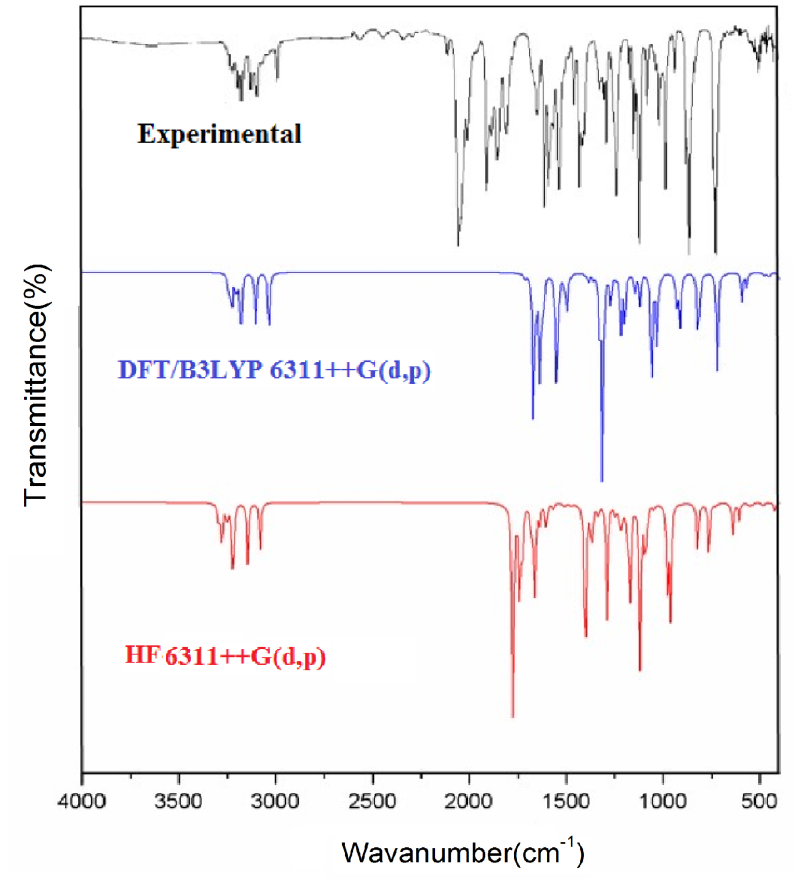
Fig. 4 Experimental and theoretical FT-IR spectra.

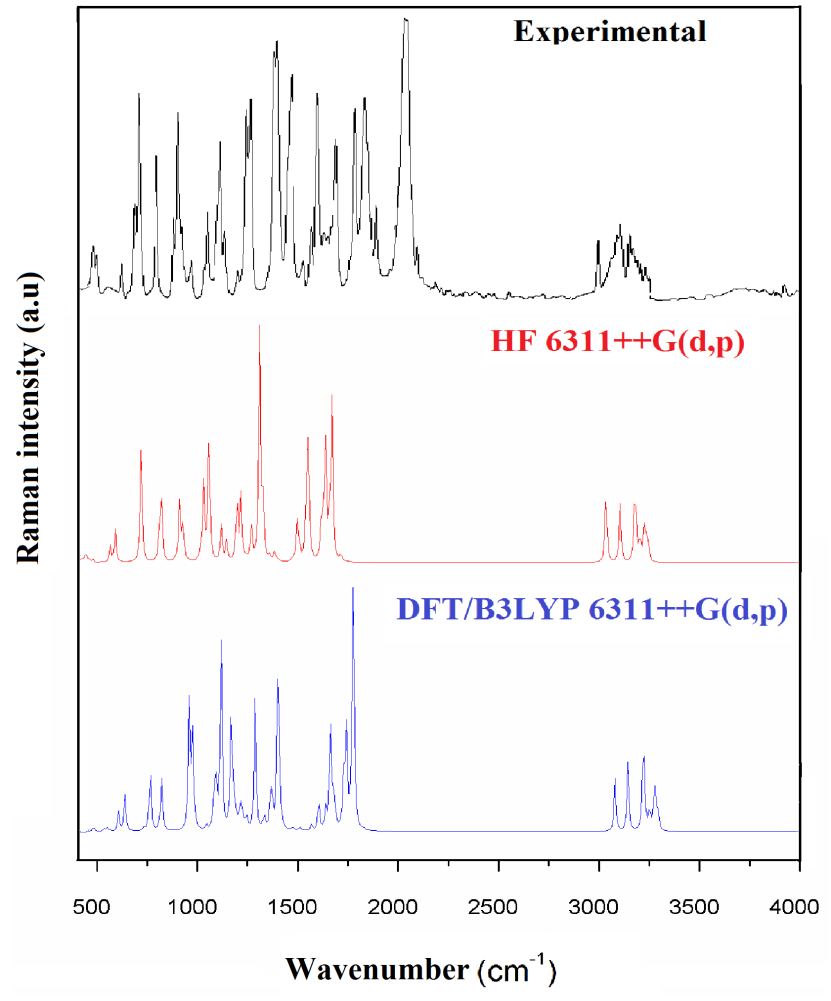
Fig. 5 Experimental and theoretical FT-Raman spectra.

Table 3. Experimental Theoretical harmonic frequencies (cm^-1) of the 3C3'MS molecule along with the assignments of vibrational modes basing on PED results.

ν→Stretching, β→ Bending, τ→torsion, δ→Out-of-plane bending, β_ipd→in-plane bending, R→ring

4.3.1 Carbon-Hydrogen Vibrations

The C-H stretching is considered as characteristic Wavenumbers. Such differences are usually observed for C-H vibrations. The aromatic ring shows the occurrence of C-H stretching vibration modes in the range 3100-3000 cm^-1 region [42, 43], which is the normal region for ready identification of C-H stretching vibrations. The title compounds observed C-H stretching vibration modes are assigned 3082,3053,3011,2984 cm^-1 in FT-IR and 3079, 3060, 2983 cm^-1in FT-Raman spectra. The Calculated scaled DFT/6311++G (d, p) and HF Values are 3103,3032,2710,2773 cm^-1 and 3142,3078,2824,2754 cm^-1 have been assigned to C-H stretching vibrations respectively.

4.3.2 Methyl group Vibrations

The Methyl group vibration modes for the assignments of CH₃ group frequencies, fundamentally nine normal vibration modes can be associated to each Methyl group [44] namely, CH₃ ss– symmetric stretch, CH₃ ips– in-plane stretch , CH₃ ops – out-of-plane stretch, CH₃ ipb – in-plane bending , CH₃ opb-out-of-plane bending , CH₃ ops – out-of-plane stretch,CH₃ ipr – in-plane rocking , CH₃ opr-out-of-plane rocking; CH₃ ipb – in-plane bending, CH₃ out-of-plane bending modes, CH₃ sb–symmetric bending, tCH₃-twisting modes of CH₃ group vibrations would be predictable to be depolarized for A'' symmetry species. The methyl C-H vibrations appear lower frequencies then aromatic C-H stretching vibrations.  The calculated Scaled DFT and HF of in-of-plane bending and out-of-plane bending modes of CH₃ values are 3290,3276,3245 cm^-1 and 3241,3226,3199 cm^-1. The observed CH₃ opb and ipb assigned 3182,3089,3001 cm^-1 in FT-IR and 3179,3160,2996 cm^-1 FT-Raman spectra. The CH₃ group vibrations computed DFT and HF/6311++G (d, p) methods also show good agreement with recorded spectral data.

4.3.3 Chlorine -Carbon Vibrations

The characteristic Cl-C stretching mode has been assigned in the region 800-600 cm^-1 [45]. The vibrations belonging to the bond between the benzene ring and halogen atoms were worth the discussion here, since mixing of several vibrations are possible due to the lowering of the molecular symmetry, and the occurrence of heavy atoms on the periphery of molecule [46]. The present calculations place the Cl-C group stretching modes at 872,856 cm^-1 in FT-Raman and at 832,815 cm^-1 in experimental FT-Raman spectrum of the molecule. The computational frequencies were identified in DFT at 831,801 cm^-1 and 785, 713 cm^-1 (HF) are assigned to Cl-C stretching vibration show good agreement with the earlier literature [47].

4.4 Nonlinear optical properties

Nonlinear optics properties 3C3'MS were calculated using the density functional theoretical method. Nonlinear       optical properties deal with the interaction of applied electric fields with different materials. The effect is established as generation of new electric fields that differ in phase, altered in frequency, amplitude or other physical properties [48]. The theoretical calculations have been shown to be useful in the description of the structure–property relationship between the polarizability and hyperpolarizabilities characterize the response of a molecular system in an applied electric field [49]. The theoretical methodology allows the determination of NLO properties as an inexpensive way to design molecules by studying their potential before synthesis and to determine the electronic structure and vibrational contributions to the high order hyperpolarizability of the molecular structure. Theoretical study plays an important role in understanding the molecular property relationship which is able to assistance in designing novel NLO materials. Theoretically, calculated values of polarizability (α) and hyperpolarizability (β) are shown in Table (4a) and (4b). The highest values of first hyperpolarizability (β_tot) (2.705X10^-24) is obtained in the method of HF/6-311++G (d, p) level using GAUSSIAN 09W package. It is interesting to note that the first hyperpolarizability of the title compound is twenty times that of the standard NLO material urea (0.13 ×10^-30 esu) [50].

Table4 (a). Polarizability (x10^-24esu) of the 3C3'MS molecule calculated at the DFT and HF method of 6- 311++G (d, p) level.         

Table 4 (b) Hyperpolarizability β (x10^-31esu) of the 3C3'MS molecule calculated at the DFT and HF method of 6- 311++G (d, p) level.

4.5 UV-Vis Spectra Analysis

Time-dependent density functional theory (TD-DFT) calculation has been performed for 3C3'MS on the basis of completely optimized ground state molecular structure to investigate the electronic properties. The Molecules allow strong π−π* and σ –σ* electron transition in the UV-Vis range with high extinction coefficients. UV spectra analyses of 3C3'MS have been studied by computational method [51]. In order to recognize electronic transitions of the molecule, TD-DFT calculations on electronic absorption spectra in the different solvent (Acetonitrile, Methanol, Ethanol) were performed. The calculated results involving the frontier orbital energies, oscillator strengths (ƒ), absorption wavelengths (λ) and excitation energies (E) for different solvent (Acetonitrile, Methanol, Ethanol) phase are illustrated in Table (5a) and (5b) and the UV-Vis spectra of  3C3'MS is shown in Fig. 6. TD-DFT calculations expect three transitions in the near ultraviolent region for 3C3'MS molecule. As it can be seen from the UV–Vis spectra [52], absorption maximum values have been found to be 202, 241, 316 nm for Acetonitrile, 209, 241, 303 nm for Methanol, and 305,240, 206 nm Ethanol solution at TD-DFT/6-311++G (d, p) lavel theory. The absorption band of 3C3'MS at the longer observed peak at 316 nm is caused by the π−π* transition. Except for 316 nm, all the other absorption bands are mostly derived due to the observed transition from HOMO-LUMO is π−π*.

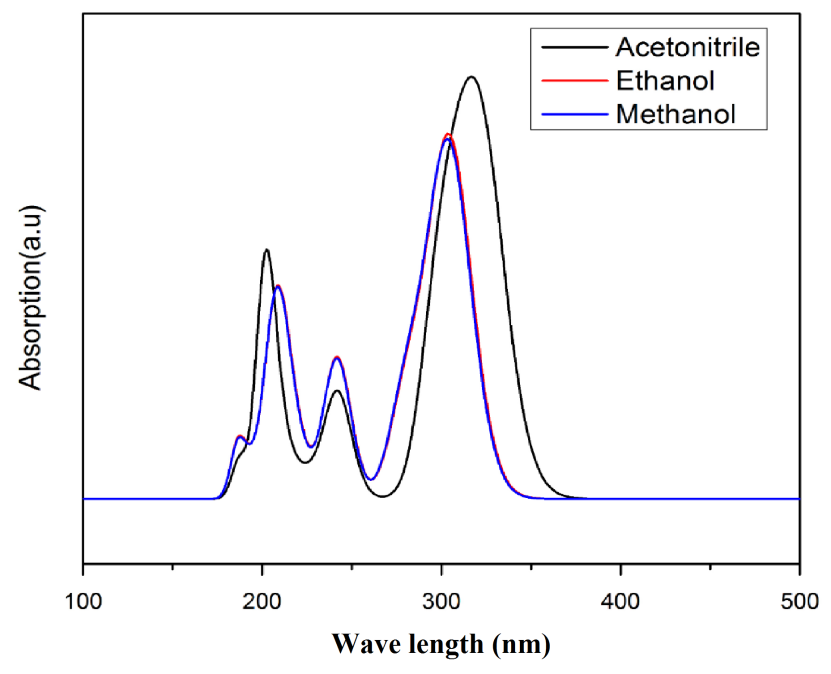
Fig. 6 Simulated UV absorption spectra.

Table 5 (a). Computed excitation energies, electronic transition configurations and oscillator strengths (f) for the optical transitions with f > 0.01 of the absorption bands in visible and near- UV region for the 3C3'MS.

Table 5 (b) Calculated Maximum absorption wavelength (λ_max), Oscillator Strength (ƒ), Excitation energy (eV) and Corresponding Electronic Transition for 3C3'MS.

4.6 Molecular Electrostatic Potential

The MEP are useful 3D plots that can be used to visualize atomic charge distributions and charge related properties of studied compound, MEP surface map was computed at DFT/6-311++G (d, p) optimized geometries.  These maps are used as a reactivity displaying most possible sites for nucleophilic and electrophilic attacks. There are useful in biological application and non-covalent interactions particularly hydrogen bonds interactions [53, 54]. The surface is related to the molecular stability and is a very useful descriptor for determining the sites for electrophilic and nucleophilic reactions, the study of biological recognition processes and hydrogen bonding interactions. In addition, they provide information on the atomic charge related properties and atomic charge distribution of molecules. The MESP is an important parameter, and their study leads to a better understanding of complex biological processes involving the dipole–dipole, charge–dipole, and quadruple–dipole interactions. The electron total density onto which the molecular electrostatic surface map has been displayed in Figs. 7a and 7b, the electron density isosurface being 0.002 a.u. Figure reveals that negative regions (blue) are mostly localized over the O atoms for the electrophilic attack and the positive regions (green) are mainly localized in the Cl-atoms for a nucleophilic attack.

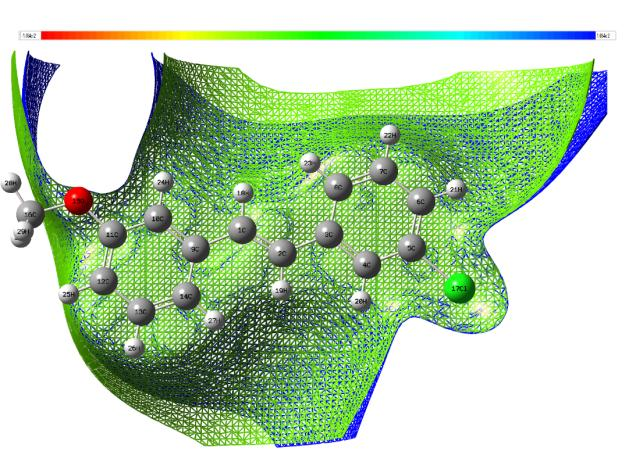
Fig. 7a Electrostatic potential contour map.

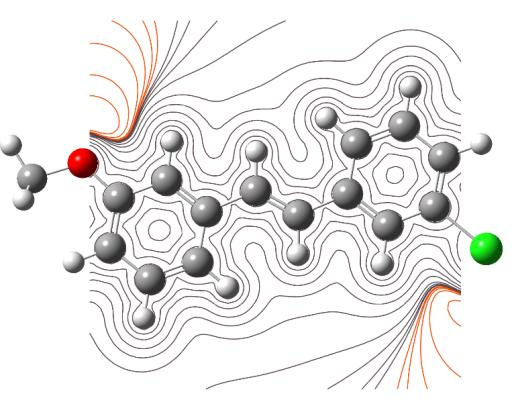
Fig. 7b Electrostatic potential contour map.

4.7 Natural Bonding Orbital’s

NBO analysis is a useful tool to investigate the highest possible percentage of the electron density between occupied Lewis-type (donor (i)) NBOs are thereby complemented by the unoccupied non-Lewis type (acceptor (j)) NBOs within the molecular system [55]. The delocalization effects can be recognized from the off-diagonal NBO Fock matrix elements of the second order Perturbation theory analysis. The interaction between occupancies of the bonding and weak occupancies of the valence anti-bonding molecular orbital energies can be qualitatively described in terms of NBO method that is expressed by means of second-order perturbation interaction energy  [55, 56]. In addition, Lewis-type (i) and non-Lewis type (j), the stabilization energy associated with i / j delocalization can be estimated as follows [56]:

Where  is the Lewis-type occupancy,   and  are diagonal elements and is the off diagonal NBO Fock matrix elements. The interaction between the  donor- acceptor and NBO Fock matrix elements [56, 57].

4.7.1 Second order Perturbation theory analysis: Donor-accepter interactions

The i - j interactions are considered by analyzing viable interactions between filled Lewis and empty non-Lewis NBOs, after approximating their molecular orbital energies through NBOs analysis. These energetic interactions are termed to as ‘delocalization’ corrections to the accurate possible natural Lewis structure. The potency of these delocalization interactions are relational to the NBO interacting intensities and molecular orbital energies which give important facts on the interactions among various parts of the molecules [58-60]. Some significant orbital intra-molecular hyper-conjugative interactions and corresponding NBO energies derived from the second order perturbation computation are listed in Table 6, which shows the most significant interactions between Lewis and non-Lewis orbital with C and O lone pairs.

Table 6. Second order perturbation theory analysis of Fock matrix of 3C3'MS by NBO method by DFT/6-311++G (d, p) method.

LR→ lone pair.

^a Stabilisation (delocalisation) energy.

^b Energy difference between i (donor) and j (acceptor) NBO orbitals.

^c Fock matrix element i and j NBO orbitals.

The intra-molecular interaction is formed by the orbital overlap of bonding between σ (C-C) and anti-bonding σ*(C-C) orbital, which results that intramolecular charge (ICT) is causing stabilization of the system.NBO analysis has been performed on the 3C3'MS molecule at the DFT/6-311++G (d, p) level in order to elucidate, the intra-molecular rehybridization and delocalization of electron density within the molecule. The most important conjugative interactions in the title molecule involving lone pair LP(1) of O15 with σ*(C11-C12), σ*(C11-C12), and of σ*(C5-C6)  with the same result in the stabilization 9.53,6.56 and 29.01 kcal/mol, respectively, and also the lone pair LP(2) of the O15 with σ*(C11-C12) with the stabilization energy of 6.56 kcal/mol. As evident from Table 6, the hyperconjugative interaction due to the orbital overlap between σ bonding orbitals of σ(2)C3-C4, σ (2)C7-C8 ,σ(2)C9-C10 and σ* anti-bonding σ*(2)C5-C6,σ*(2)C3-C4 σ*(2) C11-C12 orbitals also results in the intra-molecular charge transfer contributing to stabilization of the molecular system [61].

4.8 Mulliken Atomic Charges

The natural population charge calculation plays an important role in the application of theoretical calculation to molecular structures [62], because the atomic charges affect the electronic structure, polarizability, and much more properties of the molecular systems. The Mulliken charge distributions of the title molecule have been calculated by methods DFT/6-311++G (d,p)  and HF/6-311++G(d,p)  methods with 6-311++G (d, p) levels of theory are collected in Table 7 and the better represent in graphical chart form as given Fig. 8. From the results, It is worthy to mention that C5, C11 and Cl17 atoms of 3C3'MS exhibit more positive charges than other H atoms in an aromatic ring and carbon atoms substituted by chloride group have highest atomic charges, while the O15 atom in the molecule have negative charges which form the C3, C6 and C9 atoms. The greater electronegative (ionic) character of negative charge on O atom and positive charge on Cl atom may suggest the formation of intermolecular bonding interaction in solid forms.

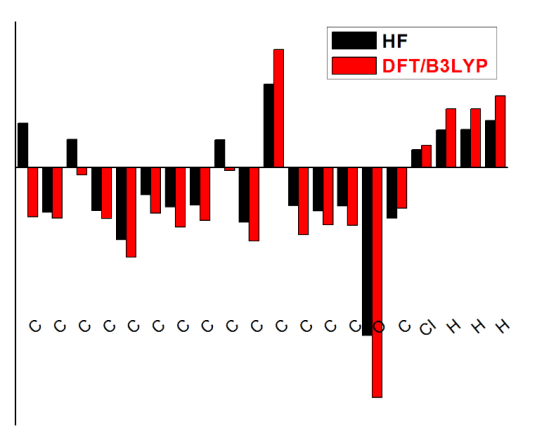
Fig. 8 Mulliken population analysis chart.

Table 7. Mulliken atomic charge analysis of 3C3'MS.

4.9 Molecular properties

The HOMO and LUMO energy values are useful descriptors in studying global reactivity of molecules and chemical hardness (h), chemical potential (µ), electronegativity (χ), electrophilicity index (ω) and softness (S). The chemical Hardness (h) is defined within the computational method as the total energy (E) with respect to the number of electrons (E) as external potential property of the system that measures both the global descriptors and molecular stability of the molecules [63].

Using Koopman’s theorem for closed-shell molecules [64], ionization potential (IP), electron affinity (EA), chemical potential, chemical hardness and softness, electrophilicity index as well as electronegativity defined [65]. The HOMO and LUMO orbital energies as IP and EA are related to the energy values of the E_HOMO and E_LUMO can be expressed as:     

Where IP and EA, Chemical Hardness (ƞ) and softness (S) [66] are known as global reactivity descriptors [67, 68] and have been theoretically justified within the background of DFT and TD-DFT [64]. These chemical descriptors-based parameters are commonly used to measure chemical reactivity and molecular properties [69]. Chemical hardness basically deals with the physical polarization of the electron cloud of the ions or molecules and atoms under small perturbation during a molecular properties and chemical reactivity [70]. Generally, soft molecules have a smaller value and the hard molecules have a larger E_HOMO and E_LUMO energy gap value [71, 72]. The computed values of the hardness, softness, chemical potential, electronegativity, and electrophilicity index, IP of donor and EA of acceptor have been calculated and the results are presented in Table 1.

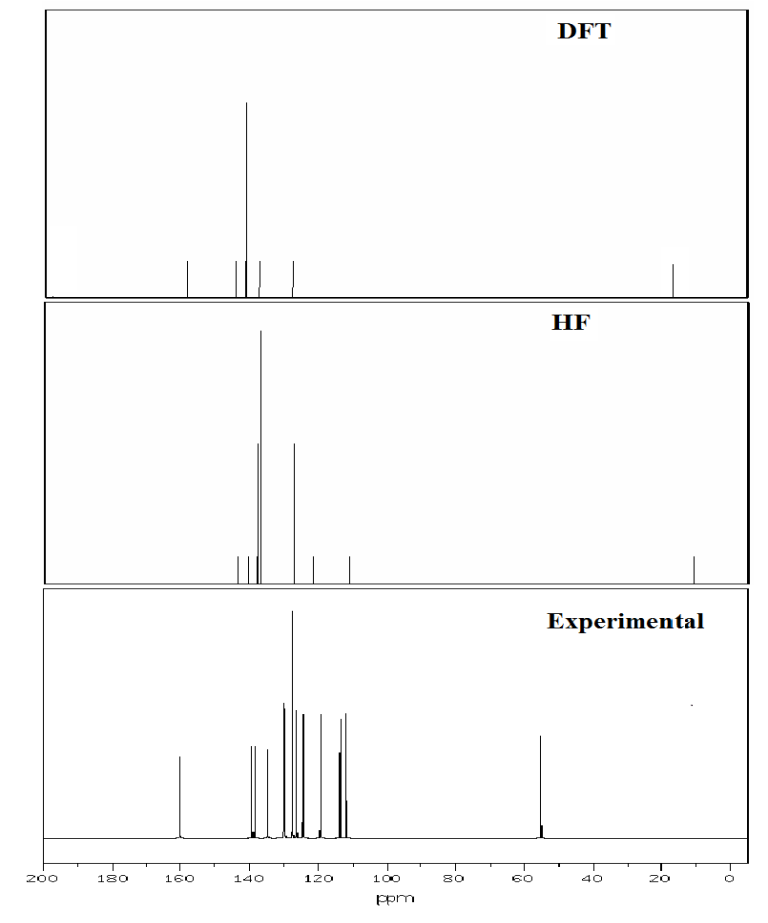
Fig. 9 Experimental and theoretical ¹³C NMR spectra.

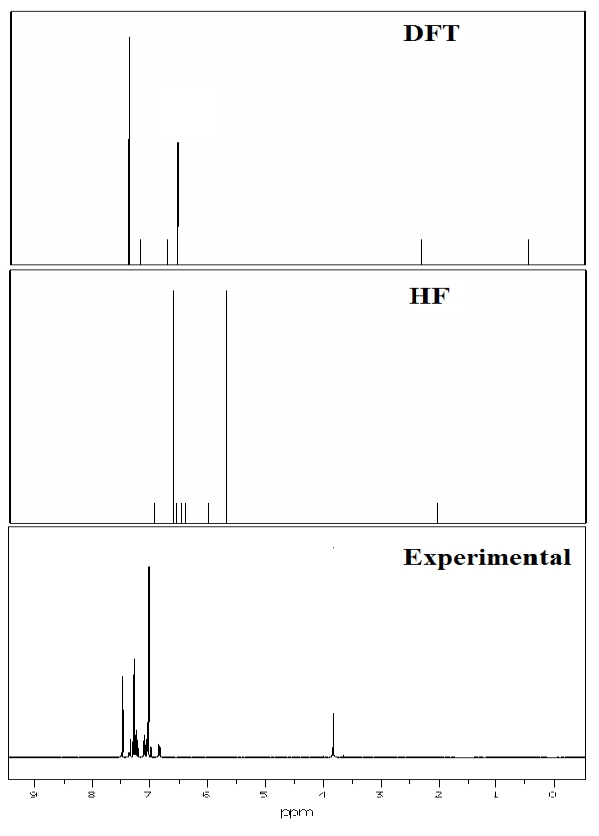
Fig. 10 Experimental and theoretical ¹H NMR spectra.

4.10 NMR Spectra analysis

The theoretical values for ¹H and ¹³C NMR Chemical shift of 3C3'MS have been compared with the excellent agreement with experimental data are listed in Table 8. The structural parameters are obtained with the DFT and HF/6-311++ G (d, p) level of theory and it is used to predict ¹H and¹³C chemical shifts with the recommended GIAO approach [73] and TMS is used for reference. The experimental and theoretical NMR spectra of the 3C3'MS molecule is shown in Figs. 9 and 10 respectively. Aromatic carbon peaks are observed from 160.01 to 56 ppm and calculated values by DFT and HF methods range from 156 to 17 and 142 to 12 ppm. The carbon atoms C16, C12, C14, C10, C8, C6, C13 and C3 are recognized to downfield NMR signals 160.01,141,139,136,130,130 and 128. These reveal the presence of partially positive charge on the carbon atoms [74]. The chemical shift (δ) value provides information on the chemical environment/magnetic properties of the protons.  Protons next to electron donating groups are shielded and protons next to electron withdrawing groups are deshielded [75]. The proton numbered H30 has the maximum chemical shift value 7.5 ppm. The 30H to 27H downfield is observed in the experimental values in ¹H with respect to calculated values. All computations are in good agreement with experimental data.  

Table 8. NMR Chemical shift (¹³C and ¹H) of 3C3'MS [δ (ppm)].

4.11 Natural Charge Analysis

Natural charges and electron population charge analysis [76] have been important role in the application of density functional calculation of molecular system. The difference of charge magnitude is in proportion with the natural charges, but they differ appreciably because this analysis includes number of core, valance and Rydberg electrons located in diffuse orbital. The development of atomic charges on the separate atom and the accumulation of electrons in the valance, core and Rydberg sub-shells are shown in Table 9. In the most electronegative charge of 0.52278 is accumulated on the oxygen atom O6 and -0.23811is accumulated on the carbon atom C4. Usually the electron cloud between bonded atoms is symmetrical, when the two atoms are similar but if one of atoms has a greater tendency to attract the electron cloud then it shifts slightly towards that atom. According to an electrostatic point of new of the molecule, these electronegative atoms have a tendency to donate an electron. Whereas, the most electropositive atoms such as; H10 have a tendency to accept an electron [77]. Further, the natural population analysis showed that 128 electrons in the 3C3'MS molecule is distributed on the sub shells as follows:

Core: 41.98304 (99.9596% of 42)

Valance: 85.81491 (99.7848% of 86)

Rydberg: 0.20205 (0.1579% of 128)

Table 9. Natural Population analysis of 3C3'MS.

4.12 Thermodynamic analysis

Thermodynamic analysis is important for understanding the chemical processes. The theoretical calculation is a well-established and efficient tool to calculate various statistical thermodynamic properties of molecular system. Nowadays, due to theoretical predictions of thermodynamic properties, and their experimental measurements are possible with high accuracy. The thermodynamic functions such as enthalpy change, heat capacity and molar entropy can be predicted easily from the molecular partition function. These calculations are used to convert molecular energy levels into macroscopic properties. Molecular energy arises from electronic excitation, Molecular translation, rotation, and vibration. This information establishes the spectroscopy of the molecule of interest [78, 79]. In the present studies, the parameters such as SCF energies, specific heat capacities, rotational constants, zero-point vibrational energies, dipole moments, rotational temperatures, 3C3'MS have been calculated at DFT and HF method with 6-311++G(d,p) basis set are listed in Table 10.

Table 10. Theoretically computed zero-point vibrational energy (Kcal mol⁻¹), rotational constants (GHz), rotational temperatures (Kelvin), thermal energy (Kcal mol⁻¹), molarcapacity at constant volume (cal mol⁻¹ Kelvin⁻¹), dipole moment (Debye) and vibrational temperatures (Kelvin) for 3C3'MS.

In this study, comparing the theoretical FT-IR, FT-Raman and Experimental FT-IR, FT-Raman spectra of the title compound 3C3'MS have been recorded. The investigations on fundamental modes along with structural, thermodynamic, electronic analysis, Natural population analysis and Mulliken population analysis of the compound have been made using ab initio DFT and HF methods with 6-311++G(d,p) basis sets. Close agreement is observed in the molecular geometries like bond lengths and bond angles calculated by DFT and HF methods. The UV-Vis spectra analysis of the molecule was also carried out. Theoretical ¹³C and ¹H chemical shift values are reported and compared with experimental data, showing a very good agreement both for ¹³C and ¹H. The HOMO–LUMO energy gap helped in analyzing the chemical reactivity of the molecule. Global hardness, softness and electrophilicity were calculated.  The FMOs have been pictured and the HOMO–LUMO energy gap has been calculated. First hyperpolarizability analysis reveals that the title compound possesses considerable NLO properties. The NBO analysis have been made with which the chemical stability and intra molecular interactions have been interpreted and the transactions give stabilization to the structure have been identified by second order perturbation energy calculations. The ESP map shows that the negative potential sites are on oxygen as well as the positive potential sites are the hydrogen and chlorine atom in a molecule.

The authors are thankful to the learned referees for their useful and critical comments, which improved the quality of the manuscript. One of the authors, M. Prakasam, acknowledges Periyar University for financial support in the form of a University Research Fellowship (URF).

Abbreviations

1. J. Saltiel, J. D.Agostino, E. D. Megarity, L. Metts, K. R. Neuberger, M. Wrighton, O. C. Zafiriou, O.L. Chapman, The cis-trans Photoisomerization of Olefins Marcel Dekker, New York, 1973.

2. D. H. Waldeck, Chem. Rev. 1991, 91, 436.

   View Article           

3. H. Meier, Angew. Chem. Int. Ed. Engl. 1992, 31, 1540.

   View Article           

4. J. S. Baskin, L. Banares, S. Pedersen, A. H. Zewail, J. Phys. Chem. 1996, 100, 11933.

   View Article           

5. P. Senthilkumar, C. Nithya and P. M. Anbarasan. J. Mol. Mod. 2013, 19, 4573. PMid:23959394

   View Article      PubMed/NCBI     

6. K.A. Muszkat, Top. Curr. Chem. 1980, 88, 143

7. T. Nakabayashi, H. Okamoto, M. Tasumi, J. Phys. Chem. 1998, 102, 9695

   View Article           

8. S. L. Schultz, J. Qian, J.M. Jean, J. Phys. Chem. 1997, 101, 1006.

   View Article           

9. R. J. Sension, A. Z. Szarka, R.M. Hochstrasser, J. Chem. Phys. 1992, 97, 5242.

   View Article           

10. J. K. Rice, A. P. Baronavski, J. Phys. Chem. 1992, 96, 3366.

    View Article           

11. H. Sanei, A. Asoodeh, S. Hamedakbari-Tusi, J. Chamani, J Solu. Chem. 2011, 40, 1905.

    View Article           

12. P. Mokaberi, V. Reyhani, Z. Amiri-Tehranizadeh, M. R. Saberi, S. Beigoli, F. Samandar and J. Chamani, New J Chem. 2019, 43, 8132.

    View Article           

13. Z. Sharif-Barfeh, S. Beigoli, S. Marouzi, A. Sharifi Rad, A. Asoodeh, J. Chamani, J. Sol. Chem. 2017, 46, 488.

    View Article           

14. M. Zolfagharzadeh, M. Pirouzi, A. Asoodeh, M.R. Saberi and J. Chamani, J. Biomol. Struc. Dynam. 2014, 32, 1936. PMid:24125112

    View Article      PubMed/NCBI     

15. J. Grundy, Chem. Rev. 1957, 57, 356.

    View Article           

16. K. Hagiwara, N. Kosaka, Y. Yoshioka, R. Takahashi ,F. Takeshita & T. Ochiya, Sci. Rep. 2012, 2, 314. PMid:22423322

    View Article      PubMed/NCBI     

17. H. A. Ali, K. Kondo, Y. Tsuda, Chem. Pharm. Bull. 1992, 40, 1136.

18. H. Matsuda, N. Tomohiro, K. Hiraba, S. Harima, S. Ko, K. Matsuo, M. Yoshikawa, M. Kubo, Bio. Pharm. Bull. 2001, 24, 267. PMid:11256482

    View Article      PubMed/NCBI     

19. S. Sanoh, S. Kitamura, K. Sugihara, N. Fujimoto, S. Ohta, J. Heal. Sci. 2003, 49, 367.

    View Article           

20. K. Tsumura, K. Furuya, A. Sakamoto, Mo. Tasumi, J. Raman Spectrosc. 2008, 39, 1591.

    View Article           

21. A. Weigel, N. P. Ernsting, J. Phys. Chem. B 2010, 114, 7893. PMid:20481560

    View Article      PubMed/NCBI     

22. R. K. Chaudhuri, J. Phys. Chem. A 2013, 117, 9434. PMid:23530611

    View Article      PubMed/NCBI     

23. A. L. Houk, I. L. Zheldakov, T. A. Tommey, and C. G. Elles, J. Phys. Chem. B 2015, 119, 9344. PMid:25369524

    View Article      PubMed/NCBI     

24. M. Arivazhagan, V. Krishnakumar, J. Xavier, G. Ilango, V. Balachandran, Spectrochimi. Acta Part A 2009, 72, 946. PMid:19196545

    View Article      PubMed/NCBI     

25. R. G.W .Yang, Density Functional Theory of Atoms and Molecular, Oxford, New York, 1989.

26. R. O .Jones, O. Gunnarson, Rev.Mol.Phys. 1989, 61, 689

    View Article           

27. T. Ziegier, Chem. Rev. 1991, 91, 651.

    View Article           

28. W. Kohn, L. J .Sham, Phys. Rev. A 1965, 140, 1133.

    View Article           

29. A. D. Becke, Phys. Rev. Part A 1988, 38, 3098 PMid:9900728

    View Article      PubMed/NCBI     

30. C .T. Lee, W.T. Yang, R.G. Parr, Phys. Rev. Part B. 1988, 37, 785. PMid:9944570

    View Article      PubMed/NCBI     

31. J. Frisch, G.W. Trucks, H.B .Schlegel, G.E .Scuseria, M.A. Robb, J.R .Cheeseman, H. Nakatsuji, M. Caricato, X. Li, H.P. Hratchian, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, R. Nakajima, Y. Honda, O. Kilao, H. Nakai, T. Verven, J. A. Montgomery Jr., J. E .Peralta, F. Ogliaro, M .Bearpark, J.J .Heyd, E. Brothers, K. N. Kudin, V. N. Staroveror, R. Kobayashi, J. Normand, K. Ragavachari, A .Rendell, J. C. Burant, S .J. Tomasi, M .Cossi, N. Rega, J.M .Millam, M. Klene, J .E Knox, J .B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R .E. Strattmann, O .Yazyev, A.J. Austin, R. Cammi, J.W. Ochetrski, R.L. Martin, K. Morokuma, V. G. Zakrazawski, G .A. Votn, P. Salvador, J.J. Dannenberg, S. Dapprich, A.D. Daniels, O. Farkas, J. B. Foresman, Gaussian O. G., Revision A.O2 Gaussian Inc., Wallingford, CT, 2009.

32. A. D .Becke, J. Chem. Phys. 1993, 98, 5652.

    View Article           

33. C. Lee, W. Yang, R. C .Parr, J. Phys. Rev. B 1998, 37, 789.

34. T. Sundius, J. Mol. Struct. 1990, 218, 326. 80287-T

    View Article           

35. Computer program Gauss View 3.09, Ver. 2 Gaussian Inc, PA, Pittsburgh, 2008.

36. P. Pulay, G. Fogarasi, F. Pang, J. E. Boggs, J. Am. Chem. Soc. 1979, 10, 2550.

    View Article           

37. G. Keresztury, J.M. Chalmers, P.R. Griffth, Raman Spectroscopy: Theory in Handbook of Vibrational Spectroscopy, John Wiley & Sons Ltd., New York, 2002.

38. M.S. Alam, D .U. Lee, J. Mol. Struc. 2017, 1128, 185.

39. M. Bakiler, I.V. Maslov, S. Akyuz, J. Mol. Struct. 1999, 475, 83. 00491-8

    View Article           

40. J. S. Murray, K .Sen, Elsevier, Amsterdam, the Netherlands, 1996.

41. J. Chamani, M. Heshmati, J Coll. Interf. Sci. 2008, 322, 119. PMid:18405913

    View Article      PubMed/NCBI     

42. V. Krishnakumar, N .Prabavathi, Spectrochim. Acta Part A 2009, 72, 747. PMid:19121975

    View Article      PubMed/NCBI     

43. G.Varsanyi, Academic Kiaclo, Budapest, 1973.

44. P.S. Kalsi, Sectroscopy of Organic Compounds New Age International P Limited Publishers, New Delhi, 2005.

45. V. Balachandran, G. Santhi, V. Karpagam, A. Lakshmi, Spectrochim. Acta Part A 2013, 110, 140. PMid:23562743

    View Article      PubMed/NCBI     

46. R. A. Yadav, I .S .Sing, Indian J. Pure Appl. Phys. 1985, 23, 627.

47. K. Parimala, V. Balachandran, Spectrochim. Acta Part A 2011, 81, 723. PMid:21795105

    View Article      PubMed/NCBI     

48. Y. R. Shen, the Principles of Nonlinear Optics Wiley, New York, 1984.

49. P. Vennila, M . Govindaraju, G .Venkatesh, C . Kamal, J. Mol. Struct. 2016, 1111, 156.

    View Article           

50. M. Adant, L. Dupuis, L .Bredas, Int. J. Quantum Chem. 2004, 56, 507.

51. B. M. Wong, M. Piacenza, F. Della Sala, Phys. Chem. Chem. Phys. 2009, 11, 4508. PMid:19475168

    View Article      PubMed/NCBI