Silvia Antonia Brandán*
Tel.: +54-381-4247752; fax: +54-381-4248169;
E- mail: sbrandan@fbqf.unt.edu.ar
© 2019 Sift Desk Journals. All Rights Reserved
VOLUME: 1 ISSUE: 2
Page No: 50-85
Silvia Antonia Brandán*
Tel.: +54-381-4247752; fax: +54-381-4248169;
E- mail: sbrandan@fbqf.unt.edu.ar
Silvia Antonia Brandán*
Cátedra de Química General. Instituto de Química Inorgánica. Facultad de Bioquímica, Química y Farmacia. Universidad Nacional de Tucumán. Ayacucho 471. 4000. San Miguel de Tucumán. Tucumán. R. Argentina.
Edyta Kucharska(edyta.kucharska@ue.wroc.pl)
Silvia Antonia Brand
In this work, monomeric and dimeric species of α- and β-cellulose were vibrationally characterized by using theoretical calculations derived from the density functional theory (DFT) and the scaled quantum mechanical force field (SQMFF) methodology. Here, the experimental available FT-IR and Raman spectra and the experimental available structure for the β- form were used in order to perform the assignments of the 129 normal vibration modes for both α- and β-cellulose forms. Raman bands and shoulders at 1258, 1153, 1123, 918, 907, 897, 864, 744, 727, 721, 483 and 281 cm-1 could probably support the presence of two proposed dimeric species of cellulose in the solid state. The structural properties reveal differences between both monomeric α- and β-cellulose species mainly evidenced by their molecular electrostatic potentials. The high dipole moment values and the higher populations for the β- form could support the major proportion found experimentally for this form. The volume contraction observed for the b-dimer could be related to their lower dipole moment in solution in relation to that observed in the gas phase. The reduction of the glycosidic angles for both forms in solution support their rigid structures, as was experimentally observed. The atomic charges on the O atoms belonging to the glucopyranose rings and to the glycosidic bonds (O33) present the lower values. The NBO and AIM studies suggest the presence of α- and β-cellulose in the two media but the major quantity of H bonds predicted for the b- form and their high donor-acceptor interaction values could support their most important proportion existent of this form in the earth. Similar reactivities were found in gas phase but the a- form is more reactive in solution than the other one probably because the electrophilicity and nucleophilicity for the b-form show lower values than the α ones.
Keywords: Cellulose, molecular structure, vibrational spectra; DFT calculations, force field.
Different crystalline and amorphous cellulose structures and their derivatives were widely studied since long time by using X-ray or electron diffraction techniques. Besides, different spectroscopic methods were employed to characterize these structures being one of the most used the vibrational spectroscopy and, for this reason, only some of these studies are mentioned here [1-31]. But, so far, there are not complete assignments of their infrared and Raman spectra because these structures are strongly dependent of the cell wall of the different cellulose fibers where they are present type (wood) and the applied procedure, as clearly was reported by Popescu et al. [17] and by Szymańska-Chargot et al. [22]. For instance, Forziati and Rowen have found changes in the crystalline structure of bacterial cellulose, cotton fibers and Valonia cell wall by using infrared spectroscopy [1] while microcrystalline cellulose was extracted from cotton waste by Lokshina et al [32] or from natural fibers by Kavkler and Demšar [25]. In the latter work the authors have demonstrated that different external factors (physical, chemical or biological) modify the composition of the natural cellulosic fibers structures. Furthermore, as cellulose is a large polymers chain of glucose connected by b-acetal linkages it is necessary first to perform a very good structural analysis previous to their vibrational study. From this vibrational point of view, only the main bands observed in the infrared and Raman spectra were reported by several authors [1-7,11-14,17,18,22-27,31]. Because of the industrial importance to identify the structures of cellulose and its derivatives by using the vibrational spectroscopy, in this work a structural and vibrational study on different cellulose structures were performed in order to know their structural properties and report the complete assignments of their vibrational spectra. With these purposes, α and b-cellulose monomeric structures (two glucose units) and their corresponding dimeric species (four glucose units) were simulated and optimized in the gas phase and in aqueous solution by using the hybrid B3LYP/6-31G* calculations [33,34]. As mentioned by Higgins et al. [4] first, it is necessary to know the detailed vibrational assignment for the monomeric units in order to interpreting the polymer spectrum. After that, their atomic charges, bond orders, stabilization energies, molecular electrostatic potential (MEP) surfaces and gap energy values can be calculated in order to observe the differences among the structural properties for the two α and b-cellulose forms. All those properties were computed in gas and aqueous solution phases by using natural bond orbital (NBO) [35], atoms in molecules (AIM) [36] and frontier orbitals [37] calculations. Later, the force fields only for the isolated monomeric structures were performed employing the scaled quantum mechanical force field (SQMFF) procedure [38] with the Molvib program [39] and, by using their corresponding internal normal coordinates. The low numbers of normal vibration modes justify the study only for those two monomeric structures while for the dimeric species the vibrational analysis was performed with the aid of the GaussView program [40]. Here, the predicted IR and Raman spectra for both monomers and dimers were compared with those experimental available reported by several authors for different cellulose structures [1-3,6,14,17,23,24,32]. In general, the different reported IR spectra for cellulose structures show clearly a similar pattern of bands but the differences observed are attributed to the diverse treatments of the processed samples in order to obtain thinner fibers, as those mentioned by Tsuboi [3], Higgins et al [4] and Popescu et al [17]. The differences reported by Higgins et al [4] analyzing the influences of different factors on the positions of the bands in the IR spectra of cellulose were also observed here for both α- and β- anomers of cellulose.
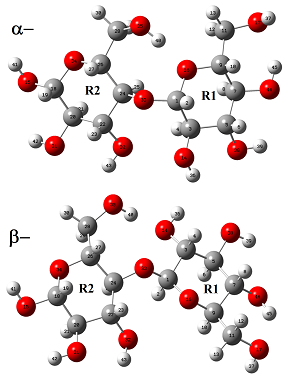
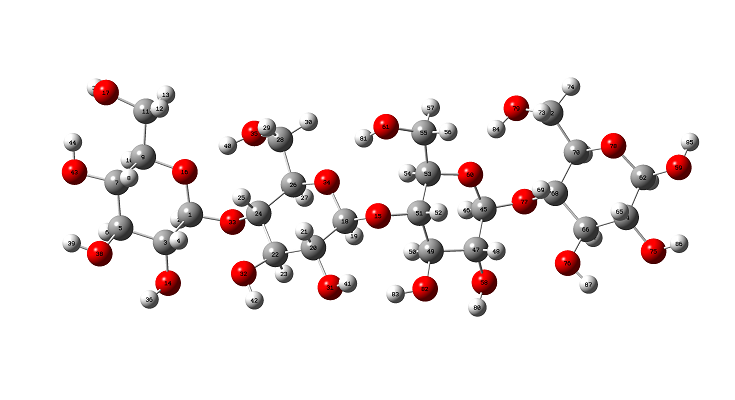
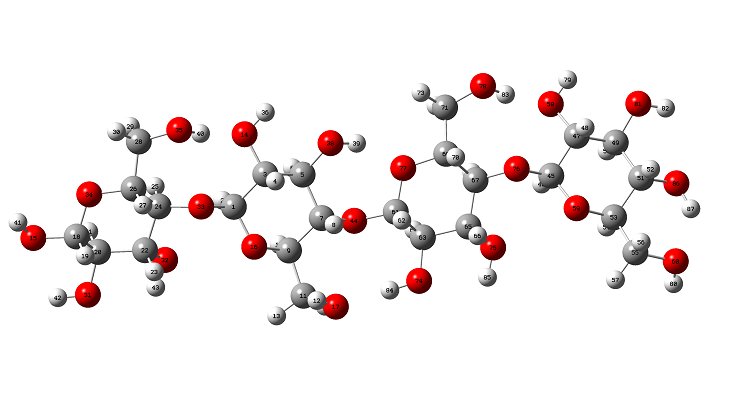
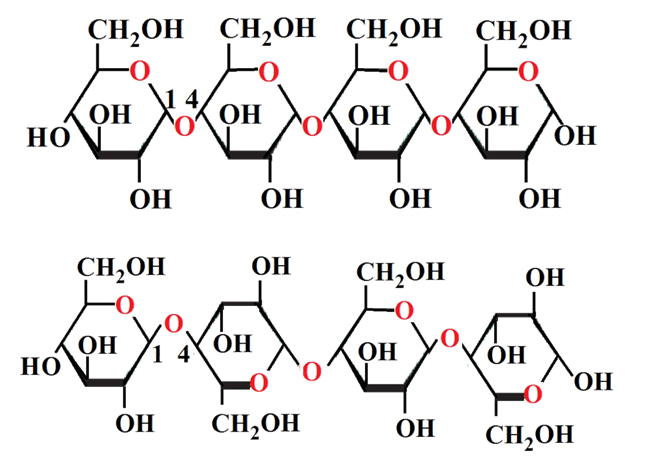
The initial structure of b-cellulose was taken from that experimental reported by Nishiyama et al [11] from Synchrotron X-ray and Neutron Fiber Diffraction. Later, the α-cellulose structure was built from that experimental b-cellulose changing the positions of the groups and taking into account that two glucose monomers have 1-4 linkage, as indicated in Figure S1 of the Supporting material. Both α- and b-cellulose monomeric structures were optimized by using the hybrid B3LYP/6-31G* method with the Gaussian 09 program [41]. After that, the dimeric species of both forms were built considering that in the α-cellulose dimeric structure the monomers have the same orientation, as can be seen in Figure S1. Figure 1 show both α- and b-cellulose monomeric structures together with the atoms labeling and the identification of their glucopyranose rings while their corresponding α- and b-cellulose dimeric species are presented in Figures 2 and 3, respectively. In aqueous solution, the self consistent reaction field (SCRF) method was used together with the polarized continuum (PCM) while the solvation energies were predicted using the solvation (SD) model with the option SMD, as implemented by the Gaussian program [42-44]. The Moldraw program [45] was employed to compute the volume variations for all the species in both media considering the differences between the values in solution in relation to the values in the gas phase. The atomic charges derived from the molecular electrostatic potential named Merz-Kollman (MK) [46] and the natural population atomic (NPA) were analyzed for the monomeric species of cellulose using the same level of theory and the NBO program [47]. On the other hand, the AIM2000 program [48] was used to compute the topological properties while the gap energies and some interesting descriptors were obtained using the HOMO-LUMO orbitals [37,49]. This way, the reactivities and behaviours of all the species were predicted using the gap values and the chemical potential (μ), electronegativity (χ), global hardness (η), global softness (S) and global electrophilicity index (ω) descriptors at the same level of theory [50-54]. Taking into account that the equations are generally known these were presented as supporting material. The force fields were computed only for the monomeric species by using the SQMFF methodology [38] and the Molvib program [39] while the internal coordinates for those cellulose species were taken of those reported for carbohydrate compounds with similar rings [55-58] and, for this reason, these were not presented in this work. The complete vibrational assignments of the monomeric cellulose structures were performed taking into account the potential energy distribution components (PED) ³ 10% while for the dimeric species the GaussView program [40] was used as an aid to perform the assignments. After that, the calculated properties for α- and b-cellulose species were analyzed and compared later with those properties reported for some compounds with similar rings, such as some carbohydrates [55-58].
Experimental available infrared and Raman spectra
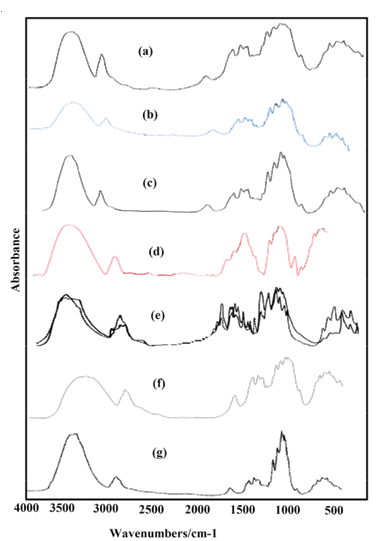
The experimental infrared spectra for microcrystalline cellulose in the 4000-400 cm-1 region were taken from Refs. [6,23,24,26,32,60,61] while the IR bands in the lower wavenumbers (400-10 cm-1) region were taken from that terahertz IR spectrum reported by the National Institute of standard and Technology in Ref [59]. Here, it is necessary to clarify that all the IR spectra recorded from different cellulose structures show practically the same profiles of bands only that in some spectra the bands have a very good definition or they are observed with major intensities than other ones, as observed in Figure S2. Obviously, the differences observed are due to the previous treatments of the processed samples. The Raman spectrum of cellulose in the solid state was taken from that reported by Søren B. Engelsen for Food Technology KVL, as indicated in Ref. [62].
4.1. Structural analysis
For the two monomeric cellulose structures and their dimeric species, the total and relative energies, dipole moments and populations calculated in gas and aqueous solution phases using the hybrid B3LYP/6-31G* level of theory can be seen in Table 1. In general, the monomeric and dimeric species show that the β- forms are the most stable in both media with higher dipole moment and population values, presenting the β-dimeric species the higher populations in both media, as obviously it is expected because the real cellulose structure is polymeric and, as a consequence the structures with four units are most stable than those with two units. The dipole moment value for the β- form in gas phase (3.67 D) is in good agreement with the value of 4.4 D reported by Agarwal et al. [63] for this form from atomistic molecular dynamics (MD) simulations. Besides, the magnitude, orientation and directions of both vector dipole moments are different from both monomeric structures, as can be seen in Figure S3. The α- form shows the vector located in a direction forming angles on the xz and yz planes while in the β- form the vector is directly on the y-axis, as observed in Figure S3 and, as reported by Agarwal et al. [63] because the cellulose polymer consists of alternating glucose units with 180◦ flips along the y-axis.
Here, it is very important to clarify that the OH and CH2OH groups belonging to the R2 rings in both forms remain without change while the CH2OH groups belonging to the R1 rings change their positions in the a and β- forms. In aqueous solution, the populations of α- monomeric forms increase significantly from 0.20 to 1.28 while the populations of the corresponding dimeric ones decrease from 0.15 to 0.00. Note that, in both monomeric and dimeric forms the higher dipole moment values are related to the most stable structures, a result also observed in other molecules [64-66]. When the energy values of two units of the β- forms in gas phase (-1297.8854 x 2= 2595.7708 Hartrees) are compared with those corresponding to the dimeric species (-2519.3660 Hartrees), a lower energy value it is observed for that dimer suggesting a higher stability for the β-form in gas phase. Similar results are obtained when the energy values for the dimers are corrected by Basis Set Superposition Error (BSSE) by using the standard Boys–Bernardi counterpoise method [67].
A comparison of calculated geometrical parameters for the two monomeric species of cellulose with the corresponding experimental ones determined for the β- form by Nishiyama et al [19] is summarized in Table 2. The root-mean-square deviation (RMSD) was used to compare the theoretical geometrical parameters with the corresponding experimental ones and the RMSD values for lengths and angles are also presented in Table 2. Thus, analyzing exhaustively these results the better concordances are obtained for the bond lengths (0.017-0.015 Å) of both forms while only for the β- form in both media it is observed lower RMSD values in the bond angles (2.9º), as compared with the α- form (3.5-3.4º). In general, the higher differences between both a- and b- structures are observed in the dihedral O17-C11-C9-O16 and O15-C18-O34-C26 angles where the B3LYP/6-31G* calculations in the two media predicted those first angles with negative signs while in the second one with positive signs, as observed in Table 2. The same signs observed for both forms in the two media are different from those experimental ones which could indicate that these changes can be dependent of the used method, as verified by us by using the wb97xd/6-31G* method. In general, the parameters for both forms show that in aqueous solution the structures practically no change and that the two forms could exist in this media, as the cellulose I structure that is a mixture of both forms with major proportion of the b- form [17,63]. But, analyzing the glycosidic C1-O33 and C24-O33 bonds in solution, it is observed that the increasing in the former bond is of 0.014 Å in α and of 0.01 Å in β while in the other one the increasing is of 0.005 Å in α and of 0.009 Å in β. This little difference in both forms in solution probably suggest that the hydrogen bonds due to the hydration or to other adjacent cellulose units restrain the flexibility of the glycosidic linkage and therefore the structures are most rigid in this medium, as reported by Bellesia et al. [20]. The reduction of the glycosidic C1-O33-C24 angles in both forms in solution support the rigid structures of both forms in solution, as observed of Table 2. At this point, it is observed that the B3LYP/6-31G* calculations underestimate the geometrical parameters, as compared with the experimental values and, that these structures can be perfectly used to perform later the vibrational analysis.
4.2. Volume variations and solvation energies
Table 3 shows the molecular volume and calculated solvation energy values for the two monomers cellulose and their dimers in different media by using the B3LYP/6-31G* method. Both monomeric species present practically the same variations in solution while higher variations and differences are observed for the dimeric species in aqueous solution, as expected due to the presence of more solvated OH groups. Whereas α- dimer present a volume expansion in solution the β dimeric form show contraction. Hence, it is evident that in the polymer exist differences between the properties of both forms. Moreover, in both monomeric species there are volume expansions in solution, as observed for sugars such as lactose and maltose [57,58]. On the other hand, the corrected solvation energy values calculated for both monomeric forms present values comparable to those observed for maltose anhydrous species (183-177 kJ/mol). In this case, it is observed that the α-form with higher volume variation present the higher solvation energy value probably because this species present higher hydration in solution, as supported by the increase in the dipole moment value (see Table 1). On the contrary, the volume contraction observed for the b-dimer could be related to their lower dipole moment in solution (8.49 D) in relation to that observed in the gas phase (8.58 D) as a consequence of higher O---O interactions in these species generating lower solvation energy. Note that the hydration increases the solvation energies as supported by the lactose [57] and maltose monohydrated [58] and sucrose di- and penta-hydrated [56].
4.3. Charges, molecular electrostatic potentials (MEP) and bond orders (BO) studies
In this work, the atomic MK and NPA charges [35,46,47] were studied by using the B3LYP/6-31G* method and, their values in both media are presented in Table S1. The calculated NPA charges on the O and H atoms present higher values than the MK charges in both media while the MK charges on the C atoms have higher values than the NPA ones, as observed in Table S1. Besides, some values on the atoms of both forms increase in solution while other decreases. Note that the NPA charges on the C11 and C28 atoms of the two cellulose forms in both media present negative signs different from the MK charges because those two atoms have positive signs. A possible explanation could be attributed to that those two C atoms belong to the CH2 groups of the side chain of both cellulose forms. Hence, the different magnitudes and orientations of the dipole moment vectors of both a- and b- forms could be strongly related to the different charges signs and positions of the CH2-OH groups because in the a-form those groups are confronted while in the b- form have opposing positions, as observed in Figure 1. On the other hand, the MK charges on the C20 atoms for the two cellulose forms in both media have negative signs different from those corresponding NPA charges. When the charges on the O atoms are analyzed those atoms belonging to the glucopyranose rings (O16 and O34) and to the glycosidic bonds (O33) present the lower charge values. In relation to the charges on the H atoms, the H13 and H29 atoms belonging to the CH2 groups and those atoms closer to the C-O bonds of both glucopyranose rings (H2, H19, H10 and H27) have low MK and NPA values.
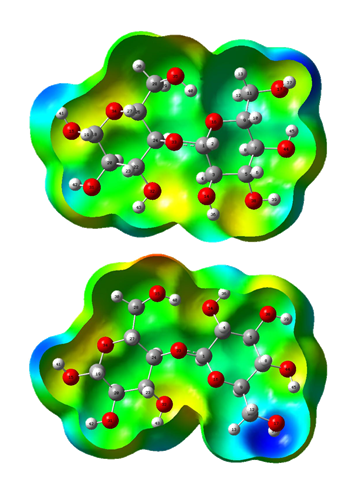
The differences between both a- and b- forms in the two media can be clearly seen when the molecular electrostatic potential values presented in Table S2 are analyzed. Thus, in both forms the O35 atoms not change their positions and, for these reasons, these atoms exhibit the higher negative MEP values while the O14 and O32 atoms present also the higher MEP values in the a- and b- forms, respectively. Regarding the H atoms, these have the less negative values, as expected, where the H37 atoms have the lower values together with the H41 and H42 atoms of both forms where these latter atoms belong to the groups OH that not change their positions while the H37 atoms have different positions in the a- and b- forms. When the mapped surfaces for these two forms are evaluated from Figure S4 it is observed that the red and blue colorations on the R2 rings of both forms remain without change while those colorations change on the R1 rings. Hence, the strong red colours are observed on the O35 atoms representing these clear nucleophilic sites (> MEP, Table S2) while the blue colours are located on the H37 atoms (< MEP, Table S2) which are electrophilic sites.
4.4. Donor-acceptor interaction, bond order (BO) and AIM study
For both cellulose structures, NBO [35,47] and AIM [36,48] calculations were performed in order to know the donor-acceptor interaction energies, the bond orders and their topological properties. Thus, Table S3 summarize the bond orders expressed as Wiberg indexes while the donor-acceptor interaction energies obtained from the second order perturbation calculations for the two monomeric species can be seen in Table S4. Analyzing first the bond orders corresponding to the atoms involved in the glycosidic linkages (C1-O33 and C24-O33) it is observed that the BO values for the O atoms are practically the same in both bonds while the BO values for the C24 atoms in both media are higher for the a- form than the values corresponding to the b- ones, in accordance with their higher MEP values forms.
Evaluating the donor-acceptor interaction energies from Table S4, it is observed that: (i) the most important interactions for both forms are observed due to the lone pairs of the O atoms, (ii) the LP(2)O16→s*O35-H40 interaction only is observed in the a-form while the LP(2)O14→s*O35-H40 interaction appear only in the b-form and, (iii) the LP(2)O14→s*C3-H4 interaction is not observed in the b-form in solution. Hence, the total energy show that the a-form is the most stable in gas phase while in solution a slight major stability it is observed for the b-form. Therefore, both forms can be seen in solution and, also, probably in the solid state, showing the b- form the major stability in both media [17,63].
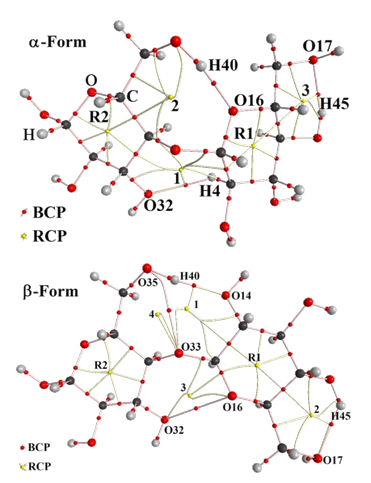
Table S5 shows the analysis of the bond critical points (BCP) for the two cellulose forms in gas and in aqueous solution phases computed by using the B3LYP/6-31G* Method. According to the Bader’s theory of atoms and molecules (AIM) [36,48], in this analysis the topological properties are calculated in order to find different interaction’s types such as the H bonds. Hence, the charge electron density, (r) and the Laplacian values, Ñ2r(r) in the bond critical points (BCPs) for both cellulose forms were calculated with the AIM2000 program [48]. This study justify the high stability of the a-form in the gas phase because for this species it is observed three H bonds interactions (three BCPs) and five ring critical points (RCPs) of which two of them belong to the glucopyranose R2 and R1 rings, as indicated in Figure S5. In solution, the stability of that form increases because in this medium are observed four BCPs and six RCPs. Note that for this form in solution appear the O14---O32 interaction while for the b-form in both media are observed two O---O interactions. Here, it is necessary to clarify that similar O---O interactions were observed in both anhydrous and monohydrated maltose species [58]. For both cellulose forms, it is observed that the calculated properties are strongly related with the distances between the atoms involved in the interactions, thus, high (r) and Ñ2r(r) values are observed for shorter distances, hence, these properties for the O14---H40 interactions observed in both forms present the higher values, as shown in Table S5. This study support the high stability of the b-form in both media and of the a-form in the gas phase.
4.5. HOMO-LUMO and descriptors studies
To predict the reactivity and behaviors of both cellulose forms in the different media is of great interest because Kavkler and Demšar [25] indicate that different external physical, chemical or biological factors have influence on the composition of the natural cellulosic fibers structures. Thus, the gap values for both cellulose forms were calculated according Parr and Pearson [37,49] in gas phase and in aqueous solution using the frontier orbitals, as can be seen in Table S6. Then, some descriptors [50-54] were also computed in order to predict the behavior of both forms and the equations used are presented in Table S6. Analyzing the gap values it is observed that both forms in gas phase have practically the same reactivities but the a- form is more reactive in solution than the other one. The comparison of these values with those calculated for trehalose (8.0-7.9 eV) [67], maltose (7.8-7.6 eV) [58] and lactose (7.5-7.2 eV) [57] shows that the reactivities of both cellulose forms are similar to those found for maltose and lactose probably because the components monosaccharides in maltose, it is glucose 1α→4glucose and in lactose, it is galactose 1β→4glucose, are similar to cellulose where are observed 1→4 linkage of α or β glucose monomers. On the other hand, analyzing the chemical potential (μ), electronegativity (χ), global hardness (η), global softness (S), global electrophilicity index (ω) and mucleophilic index (E) descriptors from Table S6 it is observed that both (ω) and (E) indexes show lower values for the b-form than the α ones. Besides, the comparison with other descriptors (Table S7) reported for different species of lactose, maltose and trehalose [57,58,68] shows that the values for both cellulose forms in the two media are similar to the anhydrous and monohydrated maltose species, possibly due to the similarity in the linkage of α or β glucose monomers.
4.6. Vibrational study
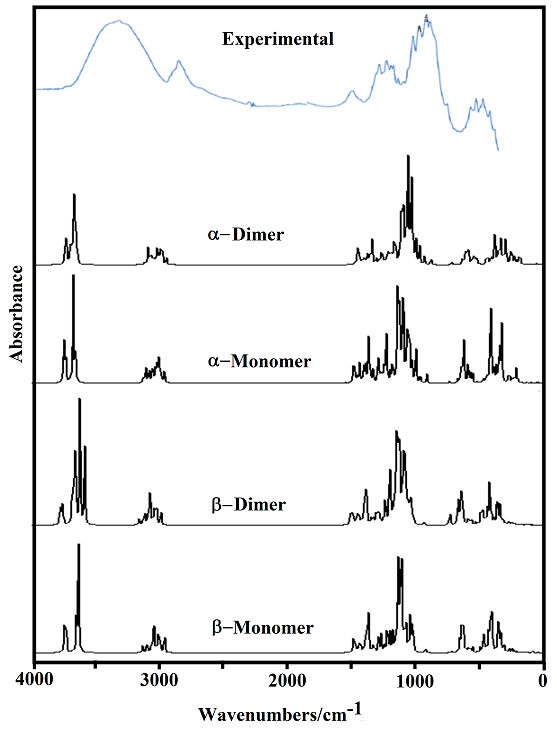
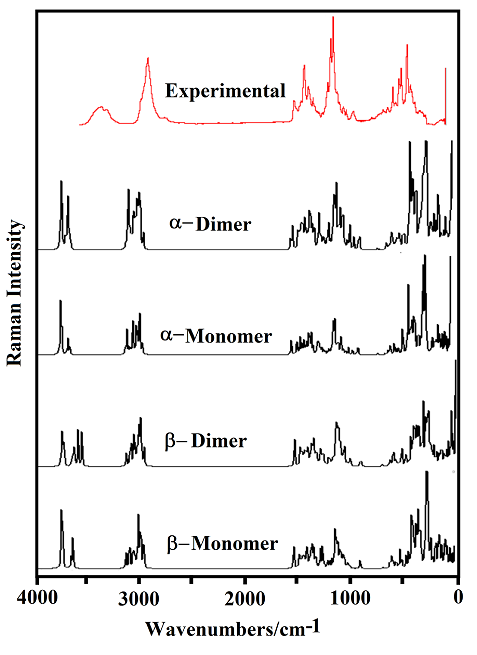
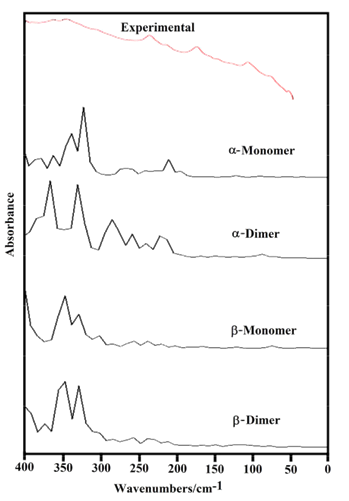
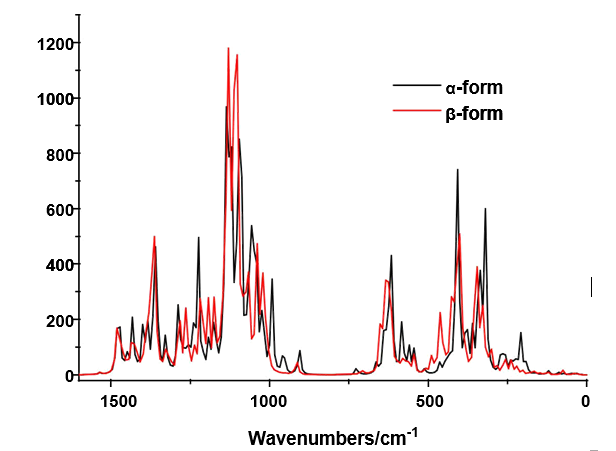
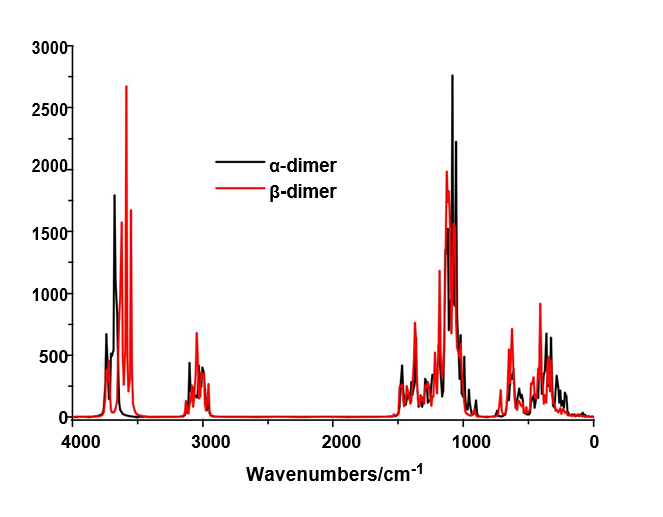
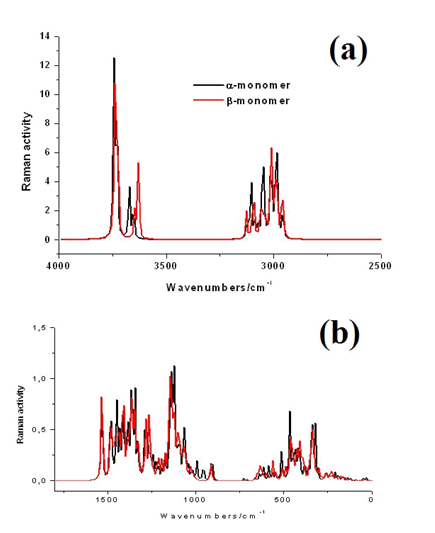
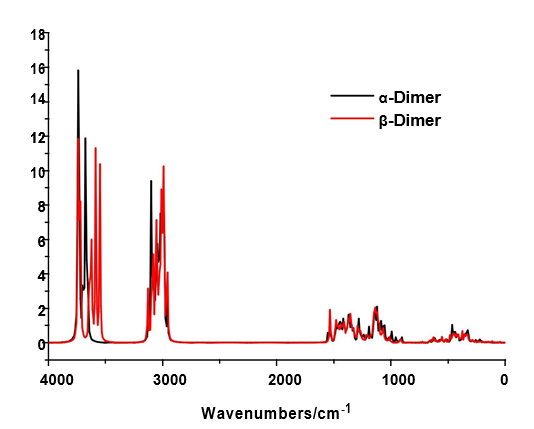
The B3LYP/6-31G* calculations predicted the two cellulose species with C1 symmetry where each monomeric species has 45 atoms and, for this reason, 129 normal vibration modes actives in the infrared and Raman spectra are expected for both forms. Figure S2 show all profiles of bands observed in different experimental available IR spectra for cellulose in the solid state reported by various authors in the 4000-400 cm-1 region [6,23,24,26,32,60,61]. In the 400-10 cm-1 region we have considered all the bands observed in the terahertz IR spectrum reported in Ref [59]. The positions of the IR and Raman bands which are summarized in Table 4 were taken from Refs. [6] and [59] and compared with bands observed in the IR spectrum from Ref [32] and in the experimental Raman according to Ref [62]. Figure 4 show the comparisons between the experimental available IR spectrum from Ref [32] and those predicted by the calculations for the a- and β-forms monomeric and dimeric species in gas phase in the 4000-0 cm-1 region. On the other hand, the comparisons between the experimental available terahertz IR spectrum taken from Ref [59] and those predicted by the calculations for the same species can be seen in Figure S6. Note that both monomeric and dimeric forms show in general approximately the same profile of bands but between the a- and β-forms clearly there are shifting and increasing in the intensities of some bands, as observed in the predicted IR spectra presented in Figures S7, S8 and S9. Hence, the observed differences among their studied properties seen in above sections. Figure 5 show the comparisons between the experimental available Raman spectrum from Ref [62] with those predicted by the calculations for the a- and β-forms monomeric and dimeric species in gas phase in the 4000-0 cm-1 region. Note the very good correlations among the predicted and experimental Raman spectra are obtained when the theoretical activities Raman for both forms, presented in Figure S10, are transformed to intensities by using the equations reported in the literature [69-71]. Figure S11 shows the predicted Raman spectra for both dimers. In Table 4 are also presented the scaled frequencies for both forms by using SQM/B3LYP/6-31G* calculations and their corresponding assignments while for the dimeric species the assignments were performed with the GaussView program [40]. The scale factors used were those reported in the literature [38] for B3LYP/6-31G* calculations. In this work, the vibrational assignments for the monomers were performed by comparison with those reported for different cellulose structures [1-7,11-14,17,18,22-27,31] and for some carbohydrates [55-58,68], and with our B3LYP/6-31G* calculations. These results can be obtained at the request of the authors. Brief discussions of the assignments for some groups are presented at continuation.
4.6.1. Band Assignments
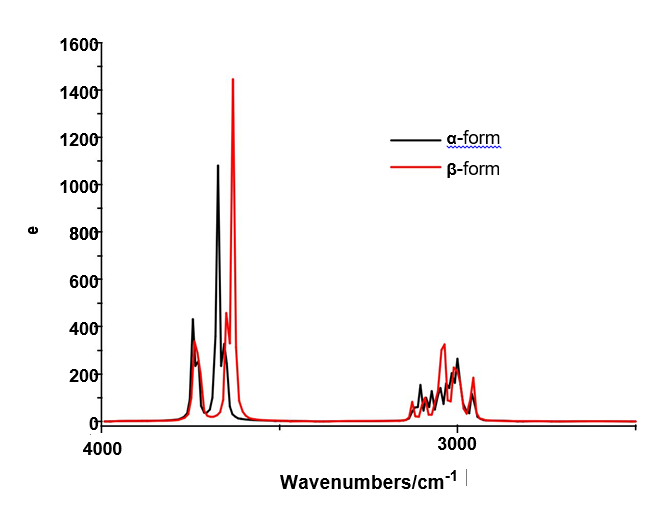
4.6.1.1. O-H modes. In this region, the broad IR bands observed in Figure 4 shows clearly that different intra and inter H bonds are expected for both cellulose forms, as reported by Guo and Wu [72], where the characteristics of both interactions are different. Here, the SQM calculations predicted the modes for both monomers between 3590 and 3480 cm-1 while for the dimers between 3742 and 3549 cm-1. Figure S7 shows clear differences between α- and β-cellulose where the most intense IR band is attributed to the intra molecular H bond O14---H40 formed in β-, as revealed by NBO and AIM analyses (Tables S4 and S5 and, Figure S5). Hence, it region is useful to identify α-cellulose from β-cellulose, as suggested by different authors [1-6,31,72,73] and, by Figs. S7 and S9. The presence of IR and Raman bands associated to both monomeric and dimeric forms suggest that all these species could exist in a crystalline cellulose sample, as reported by Kataoka and Kondo [74] where they have showed from IR spectra that the cellulose in the primary cell wall is rich in the metastable α crystalline form and present higher crystallinity than the secondary wall cellulose composed mainly of the stable β crystalline phase. Table 4 shows the detailed assignments of all the OH stretching modes corresponding to the monomeric and dimeric species. The in-plane OH deformation modes are predicted in different regions for monomer and dimers, thus, these modes can be easily assigned to the IR and Raman bands between 1397 and 1200 cm-1, as indicated in Table 4. The out-of-plane deformation modes for the two monomeric and dimeric forms are predicted in different regions, hence, for the monomers are predicted between 571 and 248 cm-1 while for the dimeric forms between 477 and 280 cm-1.Thus, they were assigned accordingly. These modes in anhydrous trehalose forms are assigned at 476-189 cm-1 while in their dihydrated species at 1389-163 cm-1 [68]. On the other hand, in anhydrous maltose these modes are assigned at 537-182 cm-1 while for the monohydrated species at 884-107 cm-1 [58].
4.6.1.2. CH modes. In the stretching CH modes there are differences between the positions of the bands associated to these modes in both α- and β-cellulose, as can be seen in Figure S7 and Table 4. Thus, the SQM calculations predicted the C24-H25, C3-H4 and C1-H2 stretching modes at higher wavenumbers for the α- form than the β- one. This shifting is in accordance with that reported for the α- anomer by Higgins et al [4] than the β- form. Note that in the dimeric forms these modes are predicted at higher wavenumbers than the monomeric ones. In the carbohydrates trehalose, maltose, lactose and sucrose these modes are expected in the respective 2997/2821, 3086/2881, 3094/2830 and 3094/2830 cm-1 regions [56-58,68]. Here, the bands observed in both spectra in the region 2911-2821 cm-1 justify clearly the presence of both monomers because the dimeric forms have not exhibit bands in this region. The rocking modes associates with these groups are assigned in the expected regions (1443-1154 cm-1), as reported by various authors [1-6,26,31] and, in accordance with some carbohydrates [56-58,68].
4.6.1.3. CH2 modes. These antisymmetric and symmetric stretching modes for both monomeric and dimeric forms are predicted by calculations in the same regions but at higher wavenumbers in the dimeric species than the other ones, as observed in Table 4. A similar relation are observed in the corresponding deformation modes of these groups, where in the dimeric species are predicted between 1535 and 1529 cm-1 while in the monomers between 1468 and 1462 cm-1. The wagging, rocking and twisting modes were assigned as predicted by SQM calculations in the 1435/1380, 1334/1173, 926/844 cm-1 regiones, respectively as indicated in Table 4 and, in accordance with those partial assignments reported [1-6,26,31]. This way, they were assigned accordingly.
4.6.1.4. Skeletal modes: The results most important of this vibrational study are observed in the C-O stretching modes belonging to the glycosidic R1>C1-O33-C24<R2 bonds and to the two glucopyranose R1 (C1-O16-C9) and R2 (C18-O34-C26) rings because these stretching modes are predicted in different regions in the α- and β- monomeric forms and, in some cases coupled with other stretching modes, as indicated in Table 4. Thus, the C1-O33 stretching modes for both forms are predicted at higher wavenumbers than the C24-O33 stretching ones with significant differences between them, thus, the separation between these modes is of approximately 229 cm-1 for the α- form while of 188 cm-1 for the β form. These results are in agreement with the bond orders corresponding to the atoms involved in the glycosidic linkages (C1-O33 and C24-O33) it is observed that the BO values for the O atoms are practically the same in both bonds while the BO values for the C24 atoms in both media are higher for the a- form than the values corresponding to the b- ones, in accordance with their higher MEP values forms. On the other hand, for the β species the stretching modes belonging to R1 rings, which are C1-O16 and C9-O16, they are predicted very closer with a difference about 36 cm-1 and, for the α- form the difference increase at 95 cm-1. Hence, the difference between both forms due to the glucopyranose R1 is evident. Analyzing, the positions of the stretching modes for R2, these are those C18-O34 and C26-O34 stretching modes, they are observed with a difference between both modes of 16 cm-1 for the α- form and of 20 cm-1 for the β- form. These results show that the rings R1 present notable modifications in the positions of the IR and Raman bands related with these modes as a consequence of the different positions of the α- and β-anomers. Regarding the C-C stretching modes in these species, it is observed from Table 4 that these modes are associated with IR and Raman bands in the 1106-669 cm-1 region as observed in the carbohydrates maltose (1171-668 cm-1) and trehalose (1131-672 cm-1) which present similar rings in their structures [58,68]. The deformation and torsions modes corresponding to both glucopyranose rings are also predicted in different positions for both anomers and, in some cases coupled with other modes. The other vibration modes expected for the α- and β- monomeric and dimeric species such as the CCC, OCO, CCO and OCC deformation modes, as summarized in Table 4.
4.7. Force Field
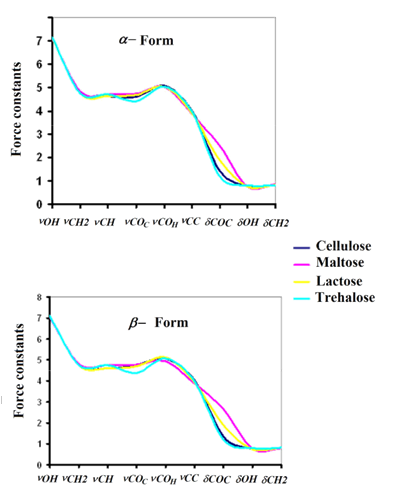
In order to analyze the different forces of the bonds, especially those related with the groups most important of both forms of cellulose the force constants were calculated by using the B3LYP/6-31G* method in gas phase employing the SQMFF procedure [38] and the Molvib program [39]. Here, the force constant values compared with those observed for carbohydrates with similar rings such as maltose [58], lactose [57] and trehalose [68] are presented in Table 5. Evaluating first the force constants for the α- and β- forms it is observed that in general the values are slightly different for both species with exception the f(nCH2), f(nC-C), f(dC-O-H) and f(dCH2) force constants that present similar values, in concordance with their frequencies observed in the vibrational analysis. The higher value observed in the f(nO-H) force constants for the α- form probably explain that for the β- form when increase the temperature decreases intensities of the bands associated to the OH groups because heating weakens hydrogen bonds, as reported by Agarwal et al [63]. On the other hand, it is very important to note that the f(dC-O-C) force constants related to the glycosidic bonds is higher in the α- form than the corresponding β- form while the f(nC-H) force constant in the α- form is higher than the other one, as expected because some frequencies corresponding to these vibration modes are observed to higher wavenumbers in the α- form than the other one. The comparisons among the force constants for the α- and β- forms of cellulose with those corresponding to maltose, lactose and trehalose [57,58,68] are presented in Figure S12. The figure clearly shows differences in the f(nC-O)C force constants related to glycosidic (C1-O33, C24-O33) bonds, to (C1-O16, C9-O16) bonds belong to R1 ring and to (C18-O34, C26-O34) bonds belong to R2 ring and, besides, to the f(dC-O-C) force constants related to the angle corresponding to glycosidic bonds. Hence, the tendency observed in both forms is: maltose > lactose > cellulose > trehalose.
In this work, monomeric and dimeric species of α- and β-cellulose were vibrationally characterized by using the experimental available FT-IR and Raman spectra and the experimental available structure for the β- form. The theoretical structures of both a- and β forms were determined at the B3LYP/6-31G* level of theory in gas and aqueous solution phases. The Raman bands and the shoulders observed in the same spectrum at 1258, 1153, 1123, 918, 907, 897, 864, 744, 727, 721, 483 and 281 cm-1 could support the presence of both proposed dimers of cellulose. Notable differences in both media were found between the structural properties studied for both monomeric α- and β-cellulose species mainly evidenced by their MEP values. The high dipole moment values and the higher populations for the β- form could support the major proportion found experimentally for this form while the direction of their vector directly on the y-axis is in accordance with the cellulose polymer. The volume contraction observed for the b-dimer could be related to their lower dipole moment in solution in relation to that observed in the gas phase, as a consequence of higher O---O interactions in these species generating lower solvation energy. The reduction of the glycosidic C1-O33-C24 angles for both forms in solution support their rigid structures, as was experimentally observed in this medium. The atomic charges on the O atoms belonging to the glucopyranose rings and to the glycosidic bonds (O33) present the lower values. The NBO and AIM studies reveal high stabilities of both forms and support their presences in the two media but the major quantity of H bonds predicted for the b- form and their high donor-acceptor interaction values could support their most important proportion existent of this form in the earth. The similar gap values in gas phase predicted the same reactivities for both forms but the a- form is more reactive in solution than the other one probably because the electrophilicity and nucleophilicity for the b-form show lower values than the α ones. Finally, complete assignments of the 129 normal vibration modes were reported for both α- and β-cellulose forms.
This work was subsidized with grants from CIUNT Project 26/D207 (Consejo de Investigaciones, Universidad Nacional de Tucumán). The authors thank Prof. Tom Sundius for his permission to use MOLVIB.
|
|
|
|
|
MK´s charges |
|
|
NPA´s charges |
|
||
|
|
Atoms |
α-form |
β-form |
α-form |
|
β-form |
||||
|
|
|
|
GAS |
PCM |
GAS |
PCM |
GAS |
PCM |
GAS |
PCM |
|
|
1 |
C |
0.628 |
0.490 |
0.741 |
0.461 |
0.410 |
0.410 |
0.408 |
0.399 |
|
|
2 |
H |
0.027 |
0.050 |
-0.028 |
-0.017 |
0.224 |
0.222 |
0.200 |
0.181 |
|
|
3 |
C |
0.043 |
0.097 |
-0.035 |
0.251 |
0.031 |
0.033 |
0.041 |
0.039 |
|
|
4 H |
0.126 |
0.120 |
0.108 |
0.097 |
0.239 |
0.231 |
0.234 |
0.260 |
|
|
|
5 |
C |
0.094 |
0.089 |
0.180 |
0.112 |
0.053 |
0.051 |
0.053 |
0.058 |
|
|
6 H |
0.054 |
0.043 |
0.040 |
0.032 |
0.216 |
0.218 |
0.218 |
0.202 |
|
|
|
7 |
C |
0.137 |
0.172 |
0.114 |
0.058 |
0.043 |
0.044 |
0.043 |
0.042 |
|
|
8 H |
0.040 |
0.045 |
0.052 |
0.065 |
0.216 |
0.219 |
0.216 |
0.221 |
|
|
|
9 |
C |
0.265 |
0.154 |
0.180 |
0.232 |
0.040 |
0.035 |
0.033 |
0.030 |
|
|
10 |
H |
-0.017 |
0.017 |
0.004 |
-0.005 |
0.212 |
0.213 |
0.208 |
0.205 |
|
|
11 |
C |
0.202 |
0.208 |
0.228 |
0.249 |
-0.113 |
-0.114 |
-0.109 |
-0.109 |
|
|
12 |
H |
0.072 |
0.082 |
0.058 |
0.052 |
0.229 |
0.232 |
0.228 |
0.231 |
|
|
13 |
H |
0.022 |
0.019 |
0.019 |
0.010 |
0.222 |
0.223 |
0.220 |
0.222 |
|
|
14 |
O |
-0.618 |
-0.596 |
-0.630 |
-0.531 |
-0.750 |
-0.746 |
-0.771 |
-0.740 |
|
|
15 |
O |
-0.623 |
-0.596 |
-0.633 |
-0.611 |
-0.755 |
-0.750 |
-0.755 |
-0.750 |
|
|
16 |
O |
-0.601 |
-0.531 |
-0.547 |
-0.516 |
-0.632 |
-0.628 |
-0.590 |
-0.587 |
|
|
17 |
O |
-0.630 |
-0.613 |
-0.627 |
-0.617 |
-0.758 |
-0.755 |
-0.761 |
-0.758 |
|
|
18 C |
0.461 |
0.450 |
0.512 |
0.538 |
0.393 |
0.391 |
0.393 |
0.390 |
|
|
|
19 |
H |
-0.018 |
-0.007 |
-0.031 |
-0.027 |
0.185 |
0.187 |
0.185 |
0.188 |
|
|
20 |
C |
-0.029 |
-0.098 |
-0.032 |
-0.146 |
0.027 |
0.026 |
0.026 |
0.026 |
|
|
21 |
H |
0.122 |
0.145 |
0.122 |
0.149 |
0.226 |
0.228 |
0.226 |
0.228 |
|
|
22 C |
0.215 |
0.280 |
0.138 |
0.243 |
0.063 |
0.063 |
0.057 |
0.057 |
|
|
|
23 |
H |
0.093 |
0.090 |
0.111 |
0.094 |
0.229 |
0.225 |
0.227 |
0.228 |
|
|
24 |
C |
0.050 |
-0.106 |
0.040 |
0.023 |
0.042 |
0.046 |
0.058 |
0.059 |
|
|
25 |
H |
0.088 |
0.115 |
0.098 |
0.088 |
0.234 |
0.231 |
0.225 |
0.219 |
|
|
26 C |
0.260 |
0.331 |
0.233 |
0.236 |
0.045 |
0.045 |
0.047 |
0.045 |
|
|
|
27 |
H |
0.036 |
0.017 |
0.043 |
0.044 |
0.223 |
0.220 |
0.223 |
0.224 |
|
|
28 |
C |
0.094 |
0.130 |
0.217 |
0.165 |
-0.104 |
-0.107 |
-0.103 |
-0.107 |
|
|
29 |
H |
0.011 |
-0.002 |
-0.015 |
-0.009 |
0.191 |
0.195 |
0.192 |
0.185 |
|
|
30 |
H |
0.090 |
0.069 |
0.055 |
0.068 |
0.227 |
0.227 |
0.224 |
0.228 |
|
|
31 |
O |
-0.630 |
-0.612 |
-0.623 |
-0.608 |
-0.768 |
-0.768 |
-0.769 |
-0.769 |
|
|
32 |
O |
-0.648 |
-0.628 |
-0.616 |
-0.597 |
-0.761 |
-0.754 |
-0.761 |
-0.760 |
|
|
33 |
O |
-0.474 |
-0.406 |
-0.477 |
-0.439 |
-0.578 |
-0.575 |
-0.581 |
-0.579 |
|
|
34 |
O |
-0.502 |
-0.499 |
-0.521 |
-0.514 |
-0.609 |
-0.610 |
-0.607 |
-0.607 |
|
|
35 |
O |
-0.611 |
-0.628 |
-0.654 |
-0.625 |
-0.767 |
-0.773 |
-0.768 |
-0.771 |
|
|
36 |
H |
0.447 |
0.425 |
0.455 |
0.356 |
0.489 |
0.487 |
0.503 |
0.476 |
|
|
37 |
H |
0.406 |
0.402 |
0.399 |
0.388 |
0.483 |
0.483 |
0.481 |
0.481 |
|
|
38 |
O |
-0.625 |
-0.625 |
-0.633 |
-0.622 |
-0.765 |
-0.764 |
-0.769 |
-0.746 |
|
|
39 |
H |
0.449 |
0.449 |
0.445 |
0.448 |
0.492 |
0.492 |
0.495 |
0.487 |
|
|
40 |
H |
0.404 |
0.413 |
0.428 |
0.383 |
0.486 |
0.485 |
0.495 |
0.494 |
|
|
41 |
H |
0.428 |
0.414 |
0.429 |
0.414 |
0.488 |
0.487 |
0.489 |
0.488 |
|
|
42 |
H |
0.440 |
0.428 |
0.436 |
0.431 |
0.492 |
0.490 |
0.492 |
0.491 |
|
|
43 |
H |
0.451 |
0.434 |
0.442 |
0.422 |
0.491 |
0.488 |
0.488 |
0.487 |
|
|
44 |
O |
-0.648 |
-0.633 |
-0.656 |
-0.644 |
-0.781 |
-0.781 |
-0.783 |
-0.786 |
|
|
45 |
H |
0.421 |
0.400 |
0.427 |
0.420 |
0.499 |
0.496 |
0.499 |
0.497 |
B3LYP/6-31G* methoda
|
|
|
α-form |
|
|
β-form |
|
|
|
Atoms |
GAS |
PCM |
GAS |
PCM |
|
|
|
1 |
C |
-14.624 |
-14.623 |
-14.629 |
-14.622 |
|
|
2 |
H |
-1.105 |
-1.104 |
-1.106 |
-1.094 |
|
|
3 |
C |
-14.691 |
-14.688 |
-14.682 |
-14.677 |
|
|
4 |
H |
-1.122 |
-1.120 |
-1.114 |
-1.105 |
|
|
5 |
C |
-14.687 |
-14.681 |
-14.681 |
-14.678 |
|
|
6 |
H |
-1.119 |
-1.111 |
-1.114 |
-1.107 |
|
|
7 |
C |
-14.680 |
-14.678 |
-14.683 |
-14.682 |
|
|
8 |
H |
-1.112 |
-1.112 |
-1.116 |
-1.116 |
|
|
9 |
C |
-14.665 |
-14.661 |
-14.675 |
-14.672 |
|
|
10 |
H |
-1.095 |
-1.090 |
-1.105 |
-1.099 |
|
|
11 |
C |
-14.666 |
-14.663 |
-14.674 |
-14.671 |
|
|
12 |
H |
-1.096 |
-1.092 |
-1.103 |
-1.100 |
|
|
13 |
H |
-1.096 |
-1.093 |
-1.104 |
-1.102 |
|
|
14 |
O |
-22.321 |
-22.324 |
-22.294 |
-22.285 |
|
|
15 |
O |
-22.291 |
-22.293 |
-22.291 |
-22.289 |
|
|
16 |
O |
-22.278 |
-22.274 |
-22.302 |
-22.299 |
|
|
17 |
O |
-22.275 |
-22.270 |
-22.280 |
-22.276 |
|
|
18 |
C |
-14.632 |
-14.633 |
-14.631 |
-14.630 |
|
|
19 |
H |
-1.110 |
-1.108 |
-1.110 |
-1.104 |
|
|
20 |
C |
-14.688 |
-14.688 |
-14.686 |
-14.682 |
|
|
21 |
H |
-1.117 |
-1.115 |
-1.116 |
-1.110 |
|
|
22 |
C |
-14.686 |
-14.688 |
-14.685 |
-14.682 |
|
|
23 |
H |
-1.121 |
-1.124 |
-1.119 |
-1.116 |
|
|
24 |
C |
-14.678 |
-14.680 |
-14.679 |
-14.674 |
|
|
25 |
H |
-1.106 |
-1.108 |
-1.109 |
-1.102 |
|
|
26 |
C |
-14.685 |
-14.689 |
-14.687 |
-14.687 |
|
|
27 |
H |
-1.120 |
-1.122 |
-1.121 |
-1.119 |
|
|
28 |
C |
-14.700 |
-14.702 |
-14.704 |
-14.703 |
|
|
29 |
H |
-1.132 |
-1.132 |
-1.136 |
-1.131 |
|
|
30 |
H |
-1.132 |
-1.134 |
-1.138 |
-1.136 |
|
|
31 |
O |
-22.303 |
-22.303 |
-22.302 |
-22.299 |
|
|
32 |
O |
-22.315 |
-22.323 |
-22.313 |
-22.313 |
|
|
33 |
O |
-22.295 |
-22.299 |
-22.295 |
-22.291 |
|
|
34 |
O |
-22.303 |
-22.309 |
-22.304 |
-22.306 |
|
|
35 |
O |
-22.337 |
-22.340 |
-22.346 |
-22.350 |
|
|
36 |
H |
-1.003 |
-1.005 |
-0.979 |
-0.970 |
|
|
37 |
H |
-0.961 |
-0.957 |
-0.966 |
-0.962 |
|
|
38 |
O |
-22.309 |
-22.303 |
-22.304 |
-22.315 |
|
|
39 |
H |
-0.992 |
-0.987 |
-0.987 |
-0.998 |
|
|
40 |
H |
-1.020 |
-1.022 |
-1.031 |
-1.033 |
|
|
41 |
H |
-0.972 |
-0.975 |
-0.972 |
-0.971 |
|
|
42 |
H |
-0.986 |
-0.986 |
-0.985 |
-0.982 |
|
|
43 |
H |
-0.997 |
-1.005 |
-0.995 |
-0.995 |
|
|
44 |
O |
-22.307 |
-22.311 |
-22.310 |
-22.313 |
|
|
45 |
H |
-0.990 |
-0.992 |
-0.992 |
-0.994 |
B3LYP/6-31G* methoda
|
|
|
α-form |
|
|
β-form |
|
|
|
Atoms |
GAS |
PCM |
GAS |
PCM |
|
|
|
1 C |
3.755 |
3.758 |
3.776 |
3.788 |
|
|
|
2 H |
0.954 |
0.955 |
0.966 |
0.973 |
|
|
|
3 C |
3.871 |
3.878 |
3.863 |
3.858 |
|
|
|
4 H |
0.948 |
0.952 |
0.951 |
0.937 |
|
|
|
5 C |
3.877 |
3.876 |
3.874 |
3.889 |
|
|
|
6 H |
0.959 |
0.958 |
0.958 |
0.965 |
|
|
|
7 C |
3.878 |
3.880 |
3.878 |
3.879 |
|
|
|
8 H |
0.959 |
0.957 |
0.959 |
0.957 |
|
|
|
9 C |
3.850 |
3.849 |
3.866 |
3.868 |
|
|
|
10 |
H |
0.961 |
0.961 |
0.964 |
0.965 |
|
|
11 |
C |
3.795 |
3.793 |
3.794 |
3.791 |
|
|
12 |
H |
0.951 |
0.949 |
0.951 |
0.950 |
|
|
13 |
H |
0.954 |
0.954 |
0.954 |
0.954 |
|
|
14 |
O |
1.794 |
1.796 |
1.797 |
1.840 |
|
|
15 |
O |
1.820 |
1.826 |
1.819 |
1.826 |
|
|
16 |
O |
1.989 |
1.995 |
2.011 |
2.013 |
|
|
17 |
O |
1.799 |
1.807 |
1.797 |
1.804 |
|
|
18 C |
3.782 |
3.785 |
3.783 |
3.785 |
|
|
|
19 |
H |
0.972 |
0.971 |
0.972 |
0.970 |
|
|
20 C |
3.871 |
3.870 |
3.871 |
3.871 |
|
|
|
21 |
H |
0.955 |
0.954 |
0.955 |
0.954 |
|
|
22 C |
3.873 |
3.878 |
3.873 |
3.874 |
|
|
|
23 |
H |
0.953 |
0.955 |
0.954 |
0.953 |
|
|
24 C |
3.858 |
3.862 |
3.853 |
3.858 |
|
|
|
25 |
H |
0.951 |
0.952 |
0.954 |
0.957 |
|
|
26 C |
3.848 |
3.852 |
3.847 |
3.850 |
|
|
|
27 |
H |
0.956 |
0.957 |
0.956 |
0.956 |
|
|
28 C |
3.830 |
3.829 |
3.833 |
3.839 |
|
|
|
29 |
H |
0.968 |
0.966 |
0.967 |
0.970 |
|
|
30 |
H |
0.951 |
0.951 |
0.953 |
0.951 |
|
|
31 |
O |
1.783 |
1.783 |
1.782 |
1.782 |
|
|
32 |
O |
1.788 |
1.791 |
1.784 |
1.783 |
|
|
33 |
O |
2.044 |
2.040 |
2.045 |
2.046 |
|
|
34 |
O |
1.995 |
1.991 |
1.995 |
1.992 |
|
|
35 |
O |
1.780 |
1.770 |
1.778 |
1.770 |
|
|
36 |
H |
0.763 |
0.765 |
0.750 |
0.776 |
|
|
37 |
H |
0.769 |
0.769 |
0.770 |
0.771 |
|
|
38 |
O |
1.783 |
1.786 |
1.780 |
1.796 |
|
|
39 |
H |
0.760 |
0.760 |
0.758 |
0.765 |
|
|
40 |
H |
0.767 |
0.768 |
0.758 |
0.759 |
|
|
41 |
H |
0.764 |
0.765 |
0.763 |
0.763 |
|
|
42 |
H |
0.760 |
0.762 |
0.760 |
0.762 |
|
|
43 |
H |
0.761 |
0.764 |
0.765 |
0.766 |
|
|
44 |
O |
1.771 |
1.766 |
1.768 |
1.762 |
|
|
45 |
H |
0.754 |
0.758 |
0.754 |
0.756 |
B3LYP/6-31G*
|
|
Delocalization |
α-form |
|
|
β-form |
|
|
|
|
GAS |
PCM |
GAS |
PCM |
|
|
|
LP(2)O14→σ*C3-H4 |
23.74 |
28.97 |
10.45 |
|
|
|
|
LP(2)O14→σ*C3-C5 |
28.67 |
21.69 |
25.25 |
27.04 |
|
|
|
LP(2)O14→σ*O35-H40 |
|
|
46.48 |
61.91 |
|
|
|
LP(2)O15→σ*C18-O34 |
59.19 |
65.67 |
58.60 |
65.71 |
|
|
|
LP(2)O16→σ*C7-C9 |
27.13 |
25.25 |
29.13 |
26.63 |
|
|
|
LP(2)O16→σ*O35-H40 |
39.08 |
49.45 |
|
|
|
|
|
LP(2)O17→σ*O44-H45 |
31.22 |
41.97 |
33.06 |
43.47 |
|
|
|
LP(2)O31→σ*C18-C20 |
32.14 |
34.53 |
32.31 |
34.28 |
|
|
|
LP(2)O32→σ*C20-C22 |
25.67 |
24.29 |
24.58 |
25.79 |
|
|
|
LP(2)O32→σ*C22-H23 |
24.87 |
26.38 |
26.04 |
23.70 |
|
|
|
LP(2)O33→σ*C1-C3 |
26.25 |
25.41 |
12.25 |
10.41 |
|
|
|
LP(2)O33→σ*C1-O16 |
54.47 |
49.78 |
60.19 |
59.19 |
|
|
|
LP(2)O33→σ*C22-C24 |
21.03 |
17.10 |
29.18 |
27.71 |
|
|
|
LP(2)O34→σ*C18-C20 |
28.13 |
26.58 |
28.59 |
26.84 |
|
|
|
LP(2)O34→σ*C24-C26 |
29.22 |
28.59 |
28.09 |
28.51 |
|
|
|
LP(2)O35→σ*C26-C28 |
37.70 |
38.12 |
40.92 |
39.12 |
|
|
|
LP(2)O38→σ*C5-H6 |
23.78 |
12.54 |
22.57 |
26.33 |
|
|
|
LP(2)O38→σ*C5-C7 |
28.22 |
34.40 |
28.84 |
26.58 |
|
|
|
LP(2)O44→σ*C7-H8 |
23.49 |
27.34 |
23.91 |
26.79 |
|
|
|
LP(2)O44→σ*C7-C9 |
30.60 |
24.83 |
30.60 |
24.62 |
|
|
|
|
|
|
|
|
|
|
|
ETotal |
142.25 |
144.23 |
141.40 |
144.65 |
|
B3LYP/6-31G* Method
α- Cellulose form
|
Parameter# |
|
Gas phase |
|
|
|
Aqueous solution/PCM |
|
||
|
O16---H40 |
O17---H45 O32---H4 |
|
O16---H40 |
O17---H45 O32---H4 O14---O32 |
|||||
|
|
|
||||||||
|
ρ(r) |
0.0304 |
0.0256 |
0.0121 |
|
0.0346 |
0.0295 |
0.0062 |
0.0073 |
|
|
∇2ρ(r) |
0.0941 |
0.0784 |
0.0437 |
|
0.1088 |
0.0886 |
0.0259 |
0.0274 |
|
|
λ1 |
-0.0444 |
-0.0346 |
-0.0125 |
|
-0.0525 |
-0.0416 |
-0.0049 |
-0.0068 |
|
|
λ2 |
-0.0423 |
-0.0311 |
-0.0103 |
|
-0.0501 |
-0.0387 |
-0.0030 |
-0.0055 |
|
|
λ3 |
0.1808 |
0.1440 |
0.0666 |
|
0.2114 |
0.1689 |
0.0338 |
0.0397 |
|
|
|λ1|/λ3 |
0.2456 |
0.2403 |
0.1877 |
|
0.2483 |
0.2463 |
0.1450 |
0.1713 |
|
|
Distances |
1.894 |
2.014 |
2.390 |
|
1.842 |
1.945 |
2.729 |
3.078 |
|
|
|
|
|
β- Cellulose form |
|
|
|
|||
|
Parameter# |
|
Gas phase |
|
|
Aqueous solution/PCM |
|
|||
|
O14---H40 |
O17---H45 O16---O32 O33---O35 O14---H40 |
O17---H45 O16---O32 O33---O35 |
|||||||
|
|
|||||||||
|
ρ(r) |
0.0268 |
0.0260 |
0.0076 |
0.0104 |
0.0342 |
0.0299 |
0.0085 |
0.0102 |
|
|
∇2ρ(r) |
0.0782 |
0.0793 |
0.0283 |
0.0440 |
0.1021 |
0.0894 |
0.0298 |
0.0432 |
|
|
λ1 |
-0.0381 |
-0.0353 |
-0.0064 |
-0.0093 |
-0.0527 |
-0.0423 |
-0.0074 |
-0.0088 |
|
|
λ2 |
-0.0369 |
-0.0319 |
-0.0050 |
-0.0042 |
-0.0505 |
-0.0393 |
-0.0068 |
-0.0037 |
|
|
λ3 |
0.1533 |
0.1466 |
0.0397 |
0.0576 |
0.2053 |
0.1711 |
0.0441 |
0.0556 |
|
|
|λ1|/λ3 |
0.2485 |
0.2408 |
0.1612 |
0.1615 |
0.2567 |
0.2472 |
0.1678 |
0.1583 |
|
|
Distances |
1.954 |
2.007 |
3.064 |
2.955 |
1.847 |
1.939 |
3.009 |
2.967 |
|
#The quantities are in atomics units, distances in Å
Monomers cellulose
|
|
Orbital |
α-form |
|
β-form |
|
|
|
|
|
|
|
|
|
|
(eV) |
GAS |
PCM |
GAS |
PCM |
|
|
|
|
|
|
|
|
|
HOMO |
-6.7160 |
-6.5981 |
-6.5604 |
-6.5141 |
|
|
LUMO |
0.9141 |
0.8123 |
1.0677 |
0.9923 |
|
|
|
|
|
|
|
|
|
GAP |
-7.6301 |
-7.4104 |
-7.6281 |
-7.5064 |
|
|
|
|
|
|
|
|
|
|
|
Descriptors (eV) |
|
|
|
|
|
|
|
|
|
|
|
χ |
-3.8151 |
-3.7052 |
-3.8141 |
-3.7532 |
|
|
|
|
|
|
|
|
|
μ |
-2.9010 |
-2.8929 |
-2.7464 |
-2.7609 |
|
|
|
|
|
|
|
|
|
η |
3.8151 |
3.7052 |
3.8141 |
3.7532 |
|
|
|
|
|
|
|
|
|
S |
0.1311 |
0.1349 |
0.1311 |
0.1332 |
|
|
|
|
|
|
|
|
|
ω |
1.1029 |
1.1293 |
0.9888 |
1.0155 |
|
|
|
|
|
|
|
|
|
Ε |
-11.0673 |
-10.7188 |
-10.4747 |
-10.3622 |
|
|
|
|
|
|
|
|
|
|
|
|
|
GAS PHASE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Trehalosea |
|
|
maltoseb |
|
|
Lactoseb |
|
||
|
Parameters |
|
Anhydrous |
|
Dihydrated |
Anhydrous |
Monohydrated |
Anhydrous |
Monohydrated |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(eV) |
αα |
αβ |
ββ |
αα |
α- |
β- |
α- |
β- |
α- |
β- |
α- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
χ |
-4.0419 |
-4.0056 |
-3.9675 |
-3.9799 |
-3.840 |
-3.895 |
-3.809 |
-3.915 |
-3.634 |
-3.625 |
-3.765 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μ |
-3.1394 |
-3.1169 |
-3.1826 |
-2.9665 |
-2.812 |
-2.801 |
-2.885 |
-2.817 |
-2.916 |
-2.982 |
-3.052 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
4.0419 |
4.0056 |
3.9675 |
3.9799 |
3.840 |
3.895 |
3.809 |
3.915 |
3.634 |
3.625 |
3.765 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
0.1237 |
0.1248 |
0.1260 |
0.1256 |
0.130 |
0.128 |
0.131 |
0.128 |
0.138 |
0.138 |
0.133 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
1.2192 |
1.2127 |
1.2765 |
1.1056 |
1.030 |
1.007 |
1.092 |
1.013 |
1.170 |
1.227 |
1.237 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ε |
-12.6888 |
-12.4847 |
-12.6270 |
-11.8064 |
-10.798 |
-10.907 |
-10.986 |
-11.029 |
-10.597 |
-10.810 |
-11.489 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aqueous solution/PCM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
χ |
-3.9298 |
-3.9263 |
-3.9105 |
-3.9021 |
-3.727 |
-3.861 |
-3.570 |
-3.881 |
-3.599 |
-3.640 |
-3.550 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μ |
-3.0970 |
-3.0729 |
-3.1596 |
-2.9905 |
-2.704 |
-2.805 |
-2.907 |
-2.993 |
-2.902 |
-3.027 |
-2.793 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
3.9298 |
3.9263 |
3.9105 |
3.9021 |
3.727 |
3.861 |
3.570 |
3.881 |
3.599 |
3.640 |
3.550 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
0.1272 |
0.1273 |
0.1279 |
0.1281 |
0.134 |
0.130 |
0.140 |
0.129 |
0.139 |
0.137 |
0.141 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
1.2203 |
1.2025 |
1.2764 |
1.1459 |
0.981 |
1.019 |
1.184 |
1.154 |
1.170 |
1.259 |
1.099 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ε |
-12.1706 |
-12.0651 |
-12.3553 |
-11.6692 |
-10.078 |
-10.830 |
-10.378 |
-11.612 |
-10.444 |
-11.018 |
-9.915 |
aFrom Ref [68], bFrom Ref. [58], cFrom ref [57]
χ = - [E(LUMO)- E(HOMO)]/2 ; μ = [E(LUMO) + E(HOMO)]/2; η = [E(LUMO) - E(HOMO)]/2;S = ½η; ω = μ2/2η
J.W. Rowen, C.M. Hunt, E.K. Plyler, Absorption Spectra in the Detection of Chemical Changes in Cellulose and Cellulose Derivatives, Journal of Research of the National Bureau of Standards, 39 (1947) 133-140.
F.H. Forziati, J.W. Rowen, Effect of Changes in Crystalline Structure on the Infrared Absorption Spectrum of Cellulose, J. Research of the National Bureau of Standards 46(1), (1951) 38-42.
View ArticleM. Tsuboi, Infrared Spectrum and Crystal Structure of Cellulose, J. Polymer Science 25 (1957) 159-171
View ArticleH.G. Higgins, C. RI. Stewart, K. J. Harrington, Infrared Spectra of Cellulose and Related Polysaccharides, J. Polymer Science 51 (1961) 59-84
View ArticleR.A. Jacobson, J.A. Wunderlich, W.N. Lipscomb, The Crystal and Molecular Structure of Cellobiose, Acta Cryst. 14 (1961) 598-607.
View ArticleJ. Blackwell, P.D. Vasko, J. L. Koenig, Infrared and Raman Spectra of the Cellulose from the Cell Wall of Valonia ventricosa, J. Applied Physics 41(11) (1970) 4375-4379.
View ArticleK.M. Paralikar, S. M. Betrabet, N.V. Bhat, The Crystal Structure of Cotton Cellulose Investigated by an Electron Diffraction Technique, J. Appl. Cryst. (1979). 12, 589-591
View ArticleB. Walsh, Identification of Cellulose Nitrate and Acetate Negatives by FTIR Spectroscopy, Topics in Photographic Preservation, 6. (1995) 80-97.
A-A. M.A. Nada, S. Kamel, M. El-Sakhawy, Thermal behaviour and infrared spectroscopy of cellulose carbamates, Polymer Degradation and Stability 70 (2000) 347-355. 00119-1
View ArticleW. Mormann, U. Michel, Improved synthesis of cellulose carbamates without by products, Carbohydrate polymers, 50 (2002) 201-208. 00016-4
View ArticleY. Nishiyama, P. Langan, H. Chanzy, Crystal Structure and Hydrogen-Bonding System in Cellulose I? from Synchrotron X-ray and Neutron Fiber Diffraction, J. Am. Chem. Soc., 124(31) (2002) 9074?9082. PMid:12149011
View Article PubMed/NCBIP. Garside, P. Wyeth, Identification of Cellulosic Fibres by FTIR Spectroscopy: Thread and Single Fibre Analysis by Attenuated Total Reflectance, Studies in Conservation, Vol. 48, No. 4 (2003), pp. 269-275.
View ArticleK. Schenzel, S. Fischer, Applications of FTRaman spectroscopy for the characterization of cellulose, Lenzinger Berichte, 83 (2004) 64-70.
M. Schwanninger, J.C. Rodrigues, H. Pereira, B. Hinterstoisser, Effects of short-time vibratory ball milling on the shape of FT-IR spectra of wood and cellulose, Vibrational Spectroscopy 36 (2004) 23-40.
View ArticleJing Wang, P. Somasundaran, Adsorption and conformation of carboxymethyl cellulose at solid?liquid interfaces using spectroscopic, AFM and allied techniques, Journal of Colloid and Interface Science 291 (2005) 75?83. PMid:15907862
View Article PubMed/NCBIC. Yin, X. Shen, Synthesis of cellulose carbamate by supercritical CO2-assisted impregnation: Structure and rheological properties, European Polymer Journal 43 (2007) 2111?2116.
View ArticleC.M. Popescu, M.C. Popescu, G. Singurel, C. vasile, D.S. Argyropoulos, S. Willfor, Spectral Characterization of Eucalyptus Wood, Applied Spectroscopy, 61(11) (2007) 1168-1177. PMid:18028695
View Article PubMed/NCBIR. Bod?rl?u, C.A. Teac?, Fourier transform infrared spectroscopy and thermal analysis of lignocellulose fillers treated with organic anhydrides, Rom. Journ. Phys., Vol. 54, Nos. 1?2, P. 93?104, Bucharest, 2009.
Y. Nishiyama, P. Langan, M. Wada, V.T. Forsyth, Looking at hydrogen bonds in cellulose, Acta Cryst. (2010). D66, 1172-1177.
View ArticleG. Bellesia, A. Asztalos, T. Shen, P. Langan, A. Redondo and S. Gnanakaran, In silico studies of crystalline cellulose and its degradation by enzymes, Acta Cryst. (2010). D66, 1184-1188
C. Driemeier, G.A. Calligaris, Theoretical and experimental developments for accurate determination of crystallinity of cellulose I materials, J. Appl. Cryst. (2011). 44, 184-192.
View ArticleM. Szyma?ska-Chargot, J. Cybulska, A. Zdunek Sensing the Structural Differences in Cellulose from Apple and Bacterial Cell Wall Materials by Raman and FT-IR Spectroscopy, Sensors 2011, 11, 5543-5560. PMid:22163913 PMCid:PMC3231429
View Article PubMed/NCBIM. Mohkami, M. Talaeipour, Investigation of the chemical structure of carboxylated and carboxymethylated fibers from waste paper via XRD and FTIR analysis, Bioresources, 6(2) (2011) 1988-2003.
D. Ciolacu, F. Ciolacu, V.I. Popa, Amorphous cellulose ? structure and characterization, Cellulose Chem. Technol., 45 (1-2) (2011) 13-21.
K. Kavkler, A. Dem?ar, Application of FTIR and Raman Spectroscopy to Qualitative Analysis of Structural Changes in Cellulosic Fibres, Tekstilec, 2012, letn. 55, ?t. 1, str. 19?31.
M. Fan, D. Dai, B. Huang, Fourier Transform Infrared Spectroscopy for Natural Fibres, Intech, Chapter 3, 2012,
View ArticleL.H. Thomas, C.M. Altaner, M.C. Jarvis, Identifying multiple forms of lateral disorder in cellulose fibres, J. Appl. Cryst. 46 (2013) 972-979.
View ArticleH. Chen, Biotechnology of Lignocellulose: Theory and Practice, DOI 10.1007/978-94-007-6898-7-2, ? Chemical Industry Press, Beijing and Springer Science CBusiness Media Dordrecht 2014.
F. Senna Vieira, C. Pasquini, Determination of Cellulose Crystallinity by Terahertz-Time Domain Spectroscopy, Anal. Chem., 86(8) (2014) 3780?3786. PMid:24654843
View Article PubMed/NCBIY. Su, C. Burger, B.S. Hsiao, B. Chu, Characterization of TEMPO-oxidized cellulose nanofibers in aqueous suspension by small-angle X-ray scattering, J. Appl. Cryst. (2014). 47, 788-798.
View ArticleL. Zhang, Z. Lu, L. Velarde, L. Fu, Y. Pu, S-Y. Ding, A.J. Ragauskas, H-F. Wang, B. Yang, Vibrational spectral signatures of crystalline cellulose using high resolution broadband sum frequency generation vibrational spectroscopy (HR-BB-SFG-VS), Cellulose, 22(3) (2015) 1469-1484.
View ArticleA.D. Becke, Density functional thermochemistry. III. The role of exact exchange, J. Chem. Phys. 98 (1993) 5648?5652.
View ArticleC. Lee, W. Yang, R.G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B 37 (1988) 785?789.
View ArticleA.E. Reed, L.A. Curtis, F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev. 88 (6) (1988) 899?926.
View ArticleR. F.W. Bader, Atoms in Molecules. A Quantum Theory, Oxford University Press, Oxford, ISBN: 0198558651, 1990.
R.G. Parr, R.G. Pearson, Absolute hardness: companion parameter to absolute electronegativity, J. Am. Chem. Soc. 105 (1983) 7512?7516.
View Articlea) G. Rauhut, P. Pulay, Transferable scaling factors for density functional derived vibrational force fields. J. Phys. Chem. 99 (1995) 3093-3099.
View Articleb) G. Rauhut, P. Pulay, J. Phys. Chem. 99 (1995) 14572.
View ArticleT. Sundius, Scaling of ab-initio force fields by MOLVIB, Vib. Spectrosc. 29, (2002) 89-95. 00189-8
View ArticleA.B. Nielsen, A.J. Holder, Gauss View 5.0, User's Reference, GAUSSIAN Inc., Pittsburgh, PA, 2008.
M.J. Frisch, G. W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G.A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H.P. Hratchian, A.F. Izmaylov, J. Bloino, G. Zheng, J.L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J.A. Montgomery, Jr., J.E. Peralta, F. Ogliaro, M. Bearpark, J.J. Heyd, E. Brothers, K. N. Kudin, V.N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J.C. Burant, S.S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J.M. Millam, M. Klene, J.E. Knox, J.B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R.E. Stratmann, O. Yazyev, A.J. Austin, R. Cammi, C. Pomelli, J.W. Ochterski, R.L. Martin, K. Morokuma, V.G. Zakrzewski, G.A. Voth, P. Salvador, J.J. Dannenberg, S. Dapprich, A.D. Daniels, O. Farkas, J.B. Foresman, J.V. Ortiz, J. Cioslowski, and D.J. Fox, Gaussian, Inc., Wallingford CT, 2009.
J. Tomasi, J. Persico, Molecular interactions in solution: an overview of methods based on continuous distributions of the solvent, Chem. Rev. 94 (1994) 2027?2094.
View ArticleS. Miertus, E. Scrocco, J. Tomasi, Electrostatic interaction of a solute with a continuum, Chem. Phys. 55 (1981) 117?129. 85090-2
View ArticleA.V. Marenich, C.J. Cramer, D.G. Truhlar, Universal solvation model based on solute electron density and a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B 113 (2009) 6378?6396. PMid:19366259
View Article PubMed/NCBIUgliengo, P. MOLDRAW Program, University of Torino, Dipartimento Chimica IFM, Torino, Italy, 1998.
B.H. Besler, K.M. Merz Jr, P.A. Kollman, J. Comp. Chem. 11 (1990) 431-439.
View ArticleE. D. Glendening, J. K.Badenhoop, A. D. Reed, J. E. Carpenter, F. Weinhold, NBO 3.1; Theoretical Chemistry Institute, University of Wisconsin; Madison, WI, 1996.
F. Biegler-K?ning, J. Sch?nbohm, D. Bayles, AIM2000; A Program to Analyze and Visualize Atoms in Molecules, J. Comput. Chem. 22 (2001) 545. 22:5<545::AID-JCC1027>3.0.CO;2-Y
View ArticleJean-Luc Bredas, Mind the gap!, Mater. Horiz.,1 (2014) 17?19.
View ArticleD. Romani, S.A. Brand?n, Structural, electronic and vibrational studies of two 1,3-benzothiazole tautomers with potential antimicrobial activity in aqueous and organic solvents. Prediction of their reactivities, Computational and Theoretical Chem., 1061 (2015) 89-99.
View ArticleM.B. M?rquez, S.A. Brand?n, A structural and vibrational investigation on the antiviral deoxyribonucleoside thymidine agent in gas and aqueous solution phases. 0020-7608. Int. J. Quantum Chem. 114(3) (2014) 209-221.
View ArticleD. Romani, S.A. Brand?n, M.J. M?rquez, M.B. M?rquez, Structural, topological and vibrational properties of an isothiazole derivatives series with antiviral activities, J. Mol. Struct. 1100 (2015) 279-289.
View ArticleD. Romani, S. Tsuchiya, M. Yotsu-Yamashita, S.A. Brand?n, Spectroscopic and structural investigation on intermediates species structurally associated to the tricyclic bisguanidine compound and to the toxic agent, saxitoxin, J. Molecular Structure 1119 (2016) 25-38.
View ArticleD. Romani, I. Salas Tonello, S.A. Brand?n, Influence of atomic bonds on the properties of the laxative drug sodium picosulphate, Heliyon (2016) 10.1016/j.heliyon.2016.e00190.
View ArticleA.B. Brizuela, L.C. Bichara, E. Romano, A. Yurquina, S. Locatelli, S.A. Brand?n, A complete characterization of the vibrational spectra of sucrose, Carbohydrate Research 361 (2012) 212-218. PMid:22878022
View Article PubMed/NCBIA.B. Brizuela, M.V. Castillo, A.B. Raschi, L. Davies, E. Romano, S.A. Brand?n, A complete assignment of the vibrational spectra of sucrose in aqueous medium based on the SQM methodology and SCRF calculations, Carbohydrate Research 388 (2014) 112-124. PMid:24632216
View Article PubMed/NCBIM.J. M?rquez, A.B. Brizuela, L. Davies, S.A. Brand?n, Spectroscopic and structural studies on lactose species in aqueous solution combining the HATR and Raman spectra with SCRF calculations, Carbohydrate Research 407 (2015) 34-41. PMid:25704196
View Article PubMed/NCBIM.A. Iramain, L. Davies, S.A. Brand?n, FTIR, HATR and FT-Raman studies on the anhydrous and monohydrate species of maltose in aqueous solution, Carbohyd. Res. 428 (2016) 41-56. PMid:27131126
View Article PubMed/NCBITerahertz Infrared Cellulose spectrum, NIST, National Institute of standard and Technology Chemistry WebBook ( ).
View ArticleInfrared Cellulose spectrum, Prepared at the 55th JECFA (2000) and published in FNP52 Add 8 (2000), superseding specifications prepared at the 51st JECFA (1998) and published in FNP52 Add 6 (1998). An Adi "not specified" was established at the 49th JECFA (1998).
R. Liu, Y. Zhang, L. Bai, M. Huang, J. Chen, Y. Zhang, Synthesis of Cellulose-2,3-bis(3,5-dimethylphenylcarbamate) in an Ionic Liquid and Its Chiral Separation Efficiency as Stationary Phase, Int. J. Mol. Sci. 15(4) (2014) 6161-6168. PMid:24733066 PMCid:PMC4013621
View Article PubMed/NCBIRaman cellulose spectrum, .
View ArticleV. Agarwal, G.W. Huber, W. Curtis Conner, Jr., S.M. Auerbach, Simulating infrared spectra and hydrogen bonding in cellulose I? at elevated temperatures, J. Chem. Phys. 135, (2011) 134506-12. PMid:21992323
View Article PubMed/NCBIE. Romano, M.V. Castillo, J.L. Pergomet, J. Zinczuk, S.A. Brand?n, Synthesis, structural and vibrational analysis of (5,7-Dichloro-quinolin-8-yloxy) acetic acid, J. Mol. Struct. 1018 (2012) 149?155.
View ArticleK. Guzzetti, A.B. Brizuela, E. Romano, S.A. Brand?n, Structural and vibrational study on zwitterions of L-threonine in aqueous phase using the FT-Raman and SCRF calculations. J. Molec. Struct. 1045 (2013) 171-179.
View ArticleS.A. Brand?n, E. Ero?lu, A.E. Ledesma, O. Oltulu, O.B. Yal??nkaya. A New vibrational study of acetazolamide compound based on normal coordinate analysis and DFT calculations, J. Mol. Struct. 993 (2011) 225-231.
View ArticleS.F. Boys, F. Bernardi, Mol. Phys. 19 (1973) 553.
View ArticleM.J. M?rquez, D. Romani, S.B. D?az, S.A. Brand?n, Submitted to Journal of King Saud University (Science), 2016.
P.L. Polavarapu, Ab initio vibrational Raman and Raman optical activity spectra, J. Phys. Chem. 94 (1990) 8106.
View ArticleG. Keresztury, S. Holly, G. Besenyei, J. Varga, A.Y. Wang, J.R. Durig, Vibrational spectra of monothiocarbamates-II. IR and Raman spectra, vibrational assignment, conformational analysis and ab initio calculations of S-methyl-N,N-dimethylthiocarbamate Spectrochim. Acta, 49A (1993) 2007-2026.
D. Michalska, R. Wysokinski, The prediction of Raman spectra of platinum(II) anticancer drugs by density functional theory, Chemical Physics Letters, 403 (2005) 211-217.
View ArticleY. Guo, P. Wu, Investigation of the hydrogen-bond structure of cellulose diacetate by two-dimensional infrared correlation spectroscopy, Carbohydrate Polymers 74 (2008) 509?513.
View ArticleR. H. Marchessault, Application of infrared spectroscopy to cellulose and wood polysaccharides, Research and development division, American Viscose Crporation, Pennsylvania, U.S.A.107-129.
Y. Kataoka, T. Kondo, FT-IR Microscopic Analysis of Changing Cellulose Crystalline Structure, during Wood Cell Wall Formation, Macromolecules 1998, 31, 760-764.
View Article