Heiner Eckert
E-mail: eckert@tum.de
© 2019 Sift Desk Journals. All Rights Reserved
VOLUME: 2 ISSUE: 2
Page No: 114-117
Heiner Eckert
E-mail: eckert@tum.de
Heiner Eckert
Technical University of Munich, Department of Chemistry, Lichtenbergstr. 4, D-85747 Garching, Germany
Heiner Eckert, Efficiency Measurement of Complex Syntheses in Chemistry and Life Sciences.(2019)Journal of Chemical Engineering And Bioanalytical Chemistry 2(2)
A synthesis efficiency algorithm is essential for the evaluation of complex syntheses in chemistry and life sciences. It must also be based on concrete and reliable criteria. Such an algorithm has been developed to precisely evaluate even highly complex syntheses and determine their synthesis efficiency Effsynt. The mathematical operations are highly suitable for electronic data processing (EDP). This algorithm can also be used as a basis for fair cost assessment of complex chemical syntheses.
Keywords: Synthesis evaluation; Synthesis efficiency; Overall yield; Complex syntheses; Multicomponent.
The ongoing and often extremely competitive upheavals in the sectors of information technology, energy, electro-mobility, biochemistry and molecular biology, mean that ecological and economical aspects of chemistry, as applicable to humans, are increasingly being focused on during this socio-economic transformation. Comprehensive efforts, including large workshops, are being undertaken in this field. [1]. The close link between chemistry and biology in life sciences is most apparent today in the synthesis of natural substances, where their biochemical variants often astound through their amazing efficiency.
We can find very similar properties in chemical synthesis in the field of multicomponent reactions (MCRs) [2-10].
An MCR is any reaction with more than two reactants.
This field has by far not received the respect due to it in main-stream chemistry, but has nevertheless been undergoing rapid development since the turn of the millennium. This is the indispensable requirement for a radical simplification of chemical synthesis [3]. It has the capability to generate synthesis processes that are equal in result to biochemical processes [2, 3] and can also occur in combination with them, for instance during the synthesis of Telaprevir by the strategic use of biocatalysis and multicomponent reactions [11].
Scheme 1: Synthesis of Ecteinascidin-743 (1) with key step Ugi-reaction U-4CR [12].
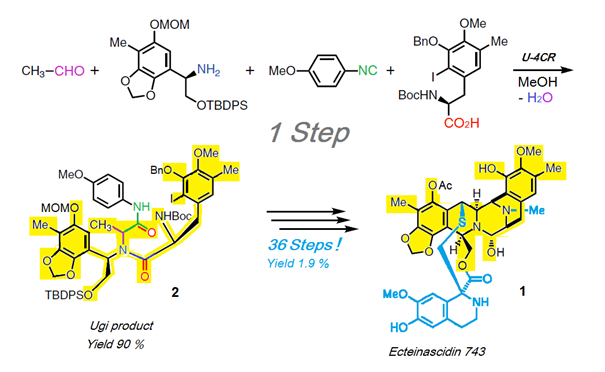
An impressive example for the high synthesis potential of MCRs in natural compound synthesis is, for example, total synthesis of the complex natural compound and anti-tumor agent Ecteinascidin-743 1 with its key step of a U-4CR based on Scheme 1 [12]. This delivers the Ugi product 2 with a 90% yield. Two-thirds of the product (24 C-atoms) and a greater part of the target product scaffold (36 C-atoms - shown here in yellow) are generated in one step. The entire reaction is presented here, together with the concentrated synthesis capacity of this U-4CR. For the rest of the synthesis another 36 conventional steps (!) are needed, which give an overall yield of 1.9 %.
The synthesis efficiency forms the core for the evaluation of innovations within the synthesis of natural products and drugs [2-5] as well is the indispensable requirement for a radical simplification of chemical synthesis [3]. Concrete and reliable criteria must be available for this purpose; criteria that can be easily determined and measured, and which can also form the basis for an algorithm. The standard evaluation of a chemical synthesis is traditionally based on the overall yield yoa. This is the product of all sequential synthesis steps yn (Eq. 1).

Synthesis of Ecteinascidins-743 [12] results in a very unsatisfactory overall yield yoa = 0.076 % over 45 steps, which does actually correspond to an average yield of 85 % per step, but which can hardly be improved any further.
This yoa directly influences the costs for the starting materials and solvents in each synthesis, but does not affect any other (fixed) costs. These fixed costs are significant and manifold, deriving from direct costs: Fixed employee and laboratory costs, laboratory rental and maintenance costs, operating costs, i.e. power, water, (gas), inert gas and disposal costs, etc. Standard repetitive laboratory activities, such as reactor configuration, filling, reaction monitoring, draining, preparation of reaction mixture and product isolation, product cleaning (distillation, recrystallisation, chromatography) and product analysis apply to all synthesis steps. The sum of these costs is similar for each synthesis step n and can be said to be constant in the first approximation in cumulo.
This provides a second concrete criterion, the synthesis step n. The efficiency of a synthesis Effsynt is defined in Eq. 2. The synthesis step n in the context of this paper is a practical unit of reaction(s) with supplements. These reactions all run in one pot in one working process without intermediate isolation/ cleaning of the reaction participants. This synthesis step therefore differs slightly from the standard definition of a reaction step.
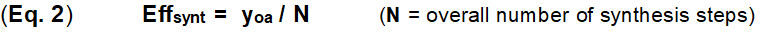
The number of steps n has a highly detrimental influence on the above-mentioned Ecteinascidin-743 synthesis (yoa = 0.076 %, N = 45, Effsynt = 0.0017 %). A brand-new total synthesis of 1 needs 26 steps, which deliver an overall yield of 1.6 % [13]. This is a great advance, but not a breakthrough in synthesis. Further examples, including the comprehensive synthesis of complex natural substances, can be found in [2, 3].
In practice, complete calculations of overall yields for complex synthesis are problematic, particularly where several precursors (2 or more) need to be included in the calculation. This is almost always the case with MCRs. All such reactions are parallel reactions and do not have any sequential character with respect to each other. Such reactions are instead cumulative, whereby the parallel reaction groups have different numbers of individual reactions n. The yields yj need to be weighted with these m values and the arithmetic mean yam calculated as shown in Eq. 3.
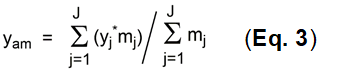
Algorithm
If you insert Eq. 1 in Eq. 3, and then insert this in Eq. 2, you will obtain the efficiency algorithm Eq. 4. This has already been generally described in [2, 3]. The weighting of the parallel reactions results in the precise value yoa.

Case study
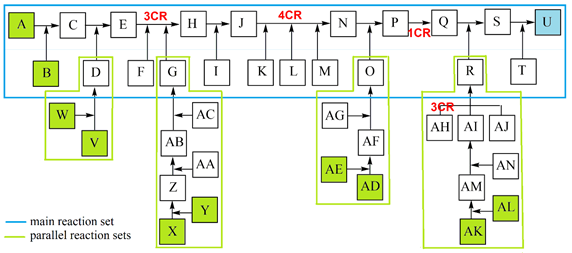
All listed and possible constellations of reactions and reaction groups in a complex synthesis are shown in a flow diagram (Scheme 2) and are presented in a detailed case study; the data were inserted into the general efficiency algorithm [2, 3]. Although publications usually only show the synthesis path with the most spectacular molecules, such as the target molecule (TM), the total synthesis with all reactions is essential for production. The quantity of potential start molecule (STM) sets also rises strongly in complex syntheses. The example shows 5 STM sets (consisting of 10 STMs) with which the synthesis can be started as well as 12 other STMs.
Scheme 2: Case study of a complex synthesis, parallel reactions. 10 STM in green, 12 STM in gray, TM U in blue.
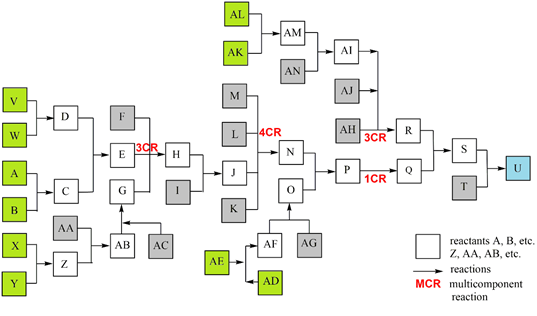
To provide a clearer overview in this study (Scheme 2), reactions are ordered to a main reaction set including two MCRs (reactants A - T, TM U), connected with 4 parallel reaction sets including a 3CR (Scheme 3).
Scheme 3: Ordered reactions of the above complex synthesis to a main reaction set and connected parallel reaction sets.
Overall yield and efficiency calculation of J in a case study
Scheme 4: Section A–J case study of Scheme 3 with operations of yoa calculation.
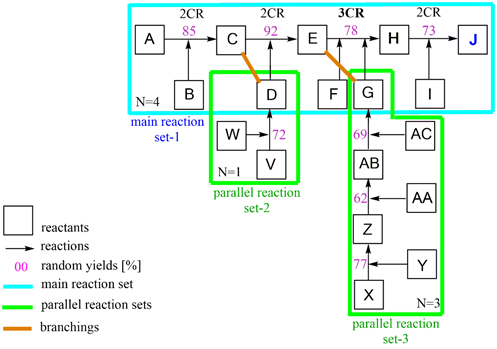
As a practical exercise, random numbers were added to the Part A - J with both parallel reactions V - D and X - G in Scheme 4. The overall yield yoa was then calculated incrementally with the algorithm in Eq. 4. Expediently, a main reaction (set-1) to which the parallel reactions are linked (set-2, set-3) is set up. The weighted arithmetical mean of the yields for each reaction set is derived at the connection forms. The overall yield yoa of the total synthesis is determined through the sequential operation of the main reaction sets. The latter can be calculated using the following calculation method.
Calculation execution
Split the main reaction set-1 at the connection points with the parallel reactions into section-1 to section-3, then use S(Pyn)j to calculate the weighted mean yield values for the two branches C,D and E,G. The latter values, together with the values from P[S(Pyn)j]k deliver the overall yield yoa of the total synthesis according to Eq. 5 - 7.
(Eq. 5) parallel reactions set-2 to main reaction position (C), operation S(Pyn)j
y(C,D) = 1/2*[y(A-C)*1 + y(V-D)*1]
= 1/2*[0.85*1 + 0.72*1] = 1/2*1.47 = 0.785
(Eq. 6) parallel reactions set-3 to main reaction position (E), operation S(Pyn)j
y(E,G) = 1/4*[y(C-E)*1 + y(X-G)*3]
= 1/4*[0.92*1 + (0.77*0.62*0.69)*3] = 1/4 [0.92 + 0.99] = 0.478
(Eq. 7) sequential main reactions set-1, operation P[S(Pyn)j]k
y(A-J) = y[(C,D)*(E,G)*(E-J) ]
= 0.785*0.478*0.78*0.73
yoa = 0.21 (21.4 %)
This synthesis consists of n = 8 synthesis steps, so the synthesis efficiency is
EffSynt = yoa / N = 0.214/8 = 0.027 (2.67 %)
The general efficiency algorithm [2,3] presented here, and the calculation methods (Eq. 3-7) developed from that algorithm, can be used to precisely evaluate even highly complex syntheses and quantitatively compare them with alternative syntheses with regards to their synthesis efficiency Effsynt. The mathematical operations are highly suitable for electronic data processing (EDP), as is the algorithm itself. The concrete criteria mean that this algorithm is also suitable as a basis for fair cost assessment of complex syntheses in chemistry and life sciences.
Energie-Effizienz Technologien in der Chemischen Industrie
View ArticleEckert, H. Molecules 2017, 22(3), 349(1-32).
Radical and Concerted Simplification of Chemical Synthesis. Ed.: Eckert, H. Wolff-Verlag: Berlin, 2017.
Eckert, H. in: MCR-2018, 7th international conference on multicomponent reactions and related chemistry: Düsseldorf, August 26th to 31st, 2018, p. 71.
Domino Reactions: Concepts for Efficient Organic Synthesis. Ed.: Tietze, L. F. Wiley-VCH: Weinheim, 2014.
Bienayme, H.; Hulme, C.; Oddon, G.; Schmitt, P.; Chem. Eur. J. 2000, 6, No.8. PMid:11039522
PubMed/NCBIDoemling, A.; Wang, Wei; Wang, Kan; Chem. Rev. 2012, 112, 3083-3135.
Doemling, A. in: Green Techniques for Organic Synthesis and Medicinal Chemistry, Chapter 18: Multicomponent Reactions. Ed.: Zhang, Wei and Berkeley, W. Cue Jr. John Wiley & Sons Ltd.: New York, 2012, pp. 497-522.
Zhu, J.; Bienayme, H. (Eds.), Multicomponent Reactions, Wiley-VCH: Weinheim, Germany, 2005.
View ArticleScience of Synthesis. Multicomponent Reactions I+II. Ed.: Mueller, T. J. J. Thieme: Stuttgart, Germany, 2014.
Znabet, A.; Polak, M. M.; Janssen, E.; de Kanter, F. J. J.; Turner, N. J.; Orru, R. V. A.; Ruijter, Chem. Commun. 2010, 46, 7918-7920. PMid:20856952
View Article PubMed/NCBIEndo, A.; Yanagisawa, A.; Abe, M.; Tohma, S.; Kan, T.; Fukuyama, T.; J. Am. Chem. Soc. 2002, 124, 6552-6554. PMid:12047173
View Article PubMed/NCBIHe, Weiming; Zhang, Zhigao; Ma, Dawei; Angew. Chem. Int. Ed. 2019, 58, accepted, doi:10.1002/anie.201900035 .
View Article