A Theoretical Study of the Chemical Reactivity of Neohesperidin Dihydrochalcone Through Conceptual DFT Descriptors

Daniel Glossman-Mitnik

Email address: daniel.glossman@cimav.edu.mx 

Juan Frau^a, Francisco Mun˜oz^a, Daniel Glossman-Mitnik^a,b,[1]

^aDepartament de Qu´ımica, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain

^bLaboratorio Virtual NANOCOSMOS, Centro de Investigaci´on en Materiales Avanzados, Chihuahua, Chih 31136, Mexico

Daniel Glossman-Mitnik, A Theoretical Study of the Chemical Reactivity of Neohesperidin Dihydrochalcone Through Conceptual DFT Descriptors(2016)SDRP Journal of Computational Chemistry & Molecular Modelling 1(2)

The Minnesota family of density functionals has been assessed for the calcula- tion of the molecular structure and properties of Neohesperidin Dihydrochalcone (NHDC) that can be an interesting sweetener with potential to act as inhibitors of the nonenzimatic glycation of amino acids and proteins, both acting as antiox- idant and perhaps as chelating agents for metallic ions, like Cu, Al and Fe. The chemical reactivity descriptors have been calculated through Conceptual DFT. The active sites for nucleophilic and electrophilic attacks have been chosen by relating them to the Fukui function indices and the dual descriptor f(2)(r). A comparison between the descriptors calculated through vertical energy values and those arising from the ?Koopmans? theorem in DFT? approximation have been performed in order to check for the validity of the last procedure and the accuracy of the studied density functionals.

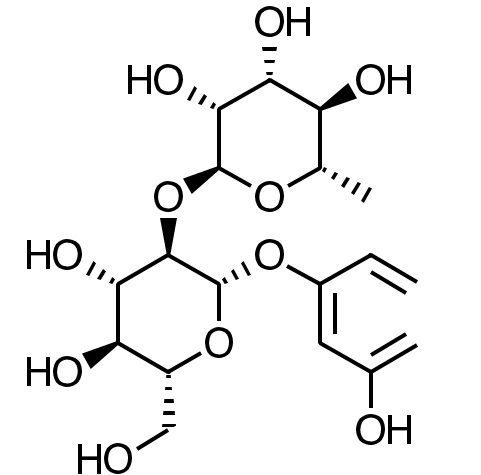
Neohesperidin dihydrochalcone (NHDC) is an intensive sweetener, obtained by alkaline hydrogenation of neohesperidin. Citrus fruits are rich sources of neohesperidin; the peels of oranges, lemons, and grapefruit contain bitter taste of neohesperidin [1].

Neohesperidin Dihydrochalcone have interesting antioxidant properties that lead to inhibition of hypochlorous acid-induced DNA strand breakage, protein degradation, and cell death [1]. Thus, it can be useful for the prevention and inhibition of the problems associated with protein degradation, like diabetes, Alzheimer and Parkinson.

Conceptual Density Functional Theory (DFT) or Chemical Reactivity Theory (as it is also known) is a powerful tool for the prediction, analysis and interpretation of the outcome of chemical reactions [2–5].

The knowledge of reactivity on a molecule is an essential concept: it is of a crucial interest because it allows to understand interactions that are operating during a reaction mechanism. In particular electrostatic interactions have been successfully explained by the use of the molecular electrostatic potential [6, 7].

On the other hand, with the aim of quantifying and understanding covalent interactions, Conceptual DFT has allowed to rationalize reaction mechanisms in terms of overlapping nucleophilic regions with electrophilic regions in order to get a maximum stabilization thus leading to final products or intermediates.

Following the pioneering work of Parr and others [2], an useful number of concepts have been derived from the analysis of the density of any molecular system through DFT. These concepts that allows a researcher to make qualitative predictions about the chemical reactivity of a given system, can also be quantified and are collectively known as Conceptual DFT Descriptors.

In order to obtain quantitative values of the Conceptual DFT Descriptors, it is necessary to resort to the Kohn-Sham theory trough calculations of the molecular density, the energy of the system, and the orbital energies, in particular, those related to the frontier orbitals, that is, HOMO and LUMO[8–13].

The usual way to proceed implies as a first step the choice of a model chemistry for the study of the molecular system or chemical reaction of interest. A model chemistry is a combination of a density functional, a basis set, and an implicit solvent model that one consider that can be adequate for the problem under study. There is a phletora of information in the literature about how to choose this model chemistry and one generally follows the experience of previous researchers and his/her own work.

Although the foundations of DFT have established that an universal density functional must exist, and that all of the properties of the system can be obtained through calculations with this functional, in practice one needs to resort to some of the approximate density functionals that have been developed during the last thirty years. Due to the fact that these are approximate functionals (that is, not an universal functionals), many of them are good for predicting some properties and others are good for another properties. Sometimes, you can find density functionals that are excellent for describing the properties of a given molecular system with a particular functional group, but it is necessary to resort to other density functionals for a different functional group that you want to include in the molecular system under study.

When one is dealing with the study of the chemical reactivity, that is, a process that involve the transference of electrons, it is usual to perform calculations not only of the ground state, but also for open systems like the radical cation and radical anion. These systems are often difficult to converge giving trustworthy results, specially if diffuse functions must be included in the basis set [8–13]. For this reason, it is convenient to have a method that can give all information that one needs directly from the results of the calculation of the ground state of the molecular system under study. In particular, one may want to obtain the ionization potential (I) and electron affinity (A) of the system avoiding the calculation of the radicals anion and cation. Indeed, the link for this s given by the so-called Koopmans’ theorem [10–13], that states that within Hartree-Fock (HF) theory, the I can be approximated by minus the energy of the HOMO, that is, I =- . By extension, it is considered that the A can be approximated by minus the energy of the LUMO, that is, A =-             .

However, the validity of the Koopmans’ theorem in DFT is controversial and the problem has been identified with the difference between the fundamental band gap and the HOMO-LUMO gap, that is called the derivative discontinuity. Notwithstanding, it has been mentioned recently [14] that an exact physical meaning can be assigned to the Kohn-Sham (KS) HOMO using ”the KS analog of Koopmans’ theorem in Hartree-Fock theory”, which states that for the exact theory, the KS HOMO is equal to and opposite of the ionization potential, _H

= -I [15–18]. Due to the mentioned problem of the discontinuity, a similar Koopmans’ theorem that relates the LUMO energy to the electron affinity does not exist. Thus, it has been proposed to circunvect the problem, to consider that the I of the N+1 electron system (the anion) is the same that the A of N electron system [14]. By considering range-separated hybrids (RSH) functionals [19–21], where the repulsive Coulomb potential is split into a long-range ( LR ) and short- range (SR) term, e.g., via r⁻¹ = r⁻¹ erf(γ r) + r⁻¹ erfc(γr), with γ the range-separation parameter, Kronik et al [14] showed that with a judicious choice of this last parameter, the validity of the Koopmans’ theorem could be enforced.

This γ tuning technique can be used for the improvement of the description of the properties predicted by these density functionals. This is a consequence of the better fullfilment of the Koopmans’ theorem that leads to better agreement of the orbital energies with the I and A. For example, Lima et al [22] have recently presented an improved description of the optical properties of carotenoids by tuning some long-range corrected functionals.

This means that the goodness of a given density functional can be estimated can be estimated by checking how well it follows the ”Koopmans’ theorem in DFT” that makes it behave closer to the exact density functional, and this will be crucial for a good calculation of the Conceptual DFT descriptors that predict and explain the chemical reactivity of molecular systems. However, the γ tuning procedure for the RSH density functionals is system dependent and that implies that different density functionals are going to be used for the calculation of the descriptors for the different molecular systems. Thus, it will be interesting to study other RSH density functionals where the γ parameter is fixed by constructions, although other parameters have been fitted to reproduce some molecular properties. In particular, we are going to consider several density functionals that have shown great accuracy across a broad spectrum of databases in chemistry and physics [23].

The aim of this work is to conduct a comparative study of the performance of the latest Minnesota family of density functionals for the description of the chemical reactivity of NHDC whose molecular structure is shown in Figure 1.

Within the conceptual framework of DFT [3, 24], the chemical potential µ, which measures the escaping tendency of electron from equilibrium, is defined

as:

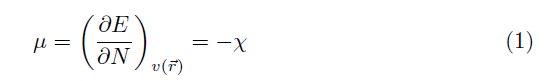
where χ is the electronegativity.

The global hardness η can be seen as the resistance to charge transfer:

Using a finite difference approximation and Koopmans’ theorem [10–13], the above expressions can be written as:

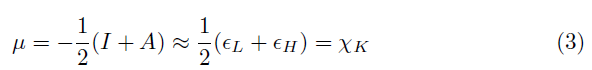
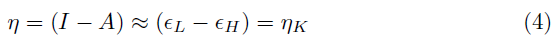
where _H and _L are the energies of the highest occupied and the lowest unoccupied molecular orbitals, HOMO and LUMO, respectively. However, within the context of density functional theory, the above inequalities are justified in light of the work of Perdew and Levy [17], where they commented on the significance of the highest occupied Kohn–Sham eigenvalue, and proved the ionization potential theorems for the exact Kohn–Sham density functional theory of a many–electron system. In addition the use of the energies of frontier molecular orbitals as an approximation to obtain I and A is supported by the Janak’s Theorem [25]. In particular, The negative of Hartree–Fock and Kohn–Sham HOMO orbital has been found to define upper and lower limits, respectively, for the experimental values of the first ionization potential [26] thus validating the use of energies of Kohn–Sham frontier molecular orbital to calculate reactivity descriptors coming from Conceptual DFT.

The electrophilicity index ω represents the stabilization energy of the systems when it gets saturated by electrons coming from the surrounding:

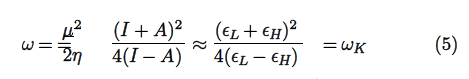
The electrodonating (ω⁻) and electroaccepting (ω⁺) powers have been defined as [27]:

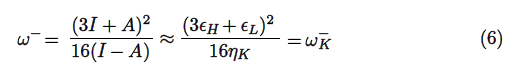
and

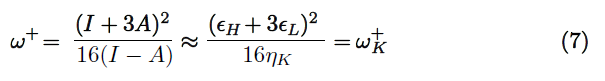
It follows that a larger ω⁺ value corresponds to a better capability of accepting charge, whereas a smaller value of ω⁻ value of a system makes it a better electron donor. In order to compare ω⁺ with -ω⁻, the following definition of net electrophilicity has been proposed [28]:

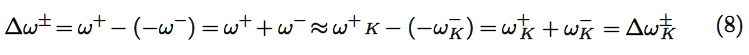
that is, the electroaccepting power relative to the electrodonating power.

At a local level, the electronic density is the first local reactivity descriptor to be used when electrostatic interactions are predominant between molecules; within the framework of Conceptual DFT it is defined as follows [2]:

But when chemical reactions are governed by interactions mainly of covalent nature, in such a case a second order LRD called Fukui function [3] is used instead of electronic density. Fukui function is defined in terms of the derivative of ρ(r) with respect to N; through a Maxwell relation, the same descriptor is interpreted as the variation of µ with respect to υ(r) [3]:

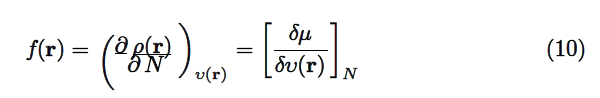
The function f(r) reflects the ability of a molecular site to accept or donate electrons. High values of f(r) are related to a high reactivity at point r [3].

Since the number of electrons N is a discrete variable [29], right and left derivatives of ρ(r) with respect to N have emerged. By applying a finite difference approximation to Eq (10), two definitions of Fukui functions depending on total electronic densities are obtained:

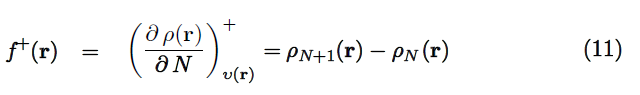
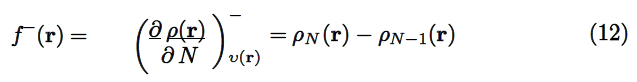
where ρ_N+1(r), ρ_N(r) and ρ_N−1(r) are the electronic densities at point r for the system with N + 1, N and N − 1 electrons, respectively. The first one, f⁺(r) , has been associated to reactivity for a nucleophilic attack so that it measures the intramolecular reactivity at the site r toward a nucleophilic reagent. The second one, f⁻(r), has been associated to reactivity for an electrophilic attack so that this function measures the intramolecular reactivity at the site r toward an electrophilic reagent [24].

Condensation to atoms is achieved through integration within the k^th–atomic domain Ω_k [30, 31]:

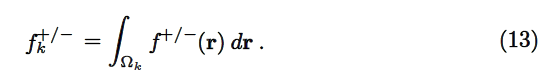
 is now an atomic index that is used to characterize the electrophilic/nucleophilic power of atom k.

Morell et al. [4, 32–37] have proposed a local reactivity descriptor ( LRD ) which is called the dual descriptor (DD) f⁽²⁾(r) ≡ ∆f(r). Mathematically it is defined in terms of the derivative of the Fukui function, f(r)[3], with respect to the number of electrons, N. The definition of f⁽²⁾(r) is shown as indicated by Morell et al. [32, 33]:

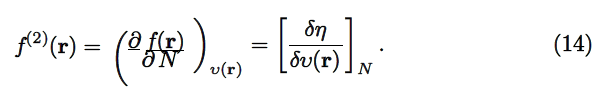
The dual descriptor can also be condensed through an appropriate integration within the k^th–atomic domain Ω_k:

Where fk(2) the process is driven by a nucleophilic attack on atom k and then that atom acts an electrophilic species; conversely, when0 the process is driven by an electrophilic attack over atom k and therefore atom k acts as a nucleophilic species.

Settings and Computational Methods

All computational studies were performed with the Gaussian 09 [38] series of programs with density functional methods as implemented in the computational package. The equilibrium geometries of the molecules were determined by means of the gradient technique. The force constants and vibrational frequencies were determined by computing analytical frequencies on the stationary points obtained after the optimization to check if there were true minima. The basis set used in this work was Def2SVP for geometry optimization and frequencies while Def2TZVP was considered for the calculation of the electronic properties [39, 40].

For the calculation of the molecular structure and properties of the studied system, we have chosen several density functionals from the Minnesota density functionals family, which consistently provide satisfactory results for several structural and thermodynamic properties [23]: M11, which is a is a rangeseparated hybrid meta-GGA[41], M11L, which is a dual-range local meta-GGA [42], MN12L, which is a nonseparable local meta-NGA [43], MN12SX, which is a range-separated hybrid nonseparable meta-NGA [44], N12, which is a nonseparable gradient approximation [45], N12SX, which is a range-separated hybrid nonseparable gradient approximation [44], SOGGA11, which is a GGA density functional [46] and SOGGA11X, which is a hybrid GGA density functional [47].

In these functionals, GGA stands for generalized gradient approximation ( in which the density functional depends on the up and down spin densities and their reduced gradient) and NGA stands for nonseparable gradient approximation (in which the density functional depends on the up/down spin densities and their reduced gradient, and also adopts a nonseparable form). All the calculations were performed in the presence of water as a solvent, by doing IEF-PCM computations according to the SMD solvation model [48].

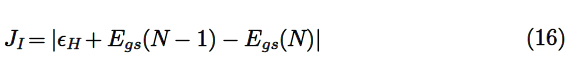
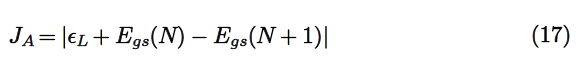
Next, we consider four other descriptors that analyze how well the studied density functionals are useful for the prediction of the electronegativity χ, the [ h ]

Table 1: HOMO and LUMO orbital energies (in eV), ionization potentials I and electron affinities A (in eV), and global electronegativity χ, total hardness η, global electrophilicity ω, electroaccepting power (ω⁺), and net electrophilicity ∆ω^± of the NHDC molecule calculated with the M11, M11L, MN12L, MN12SX, N12, N12SX, SOGGA11 and SOGGA11X density functionals and the Def2TZVP basis set using water as as solvent simulated with the SMD parametrization of the IEF-PCM model . The upper part of the table shows the results derived assuming the validity of Koopmans’ theorem and the lower part shows the results derived from the calculated vertical I and A.

Table 1: HOMO and LUMO orbital energies (in eV), ionization potentials I and electron affinities A (in eV), and global electronegativity χ, total hardness η, global electrophilicity ω, electroaccepting power (ω⁺), and net electrophilicity ∆ω^± of the NHDC molecule calculated with the M11, M11L, MN12L, MN12SX, N12, N12SX, SOGGA11 and SOGGA11X density functionals and the Def2TZVP basis set using water as as solvent simulated with the SMD parametrization of the IEF-PCM model . The upper part of the table shows the results derived assuming the validity of Koopmans’ theorem and the lower part shows the results derived from the calculated vertical I and A.

global hardness η and the global electrophilicity ω, and for a combination of these Conceptual DFT descriptors, just considering the energies of the HOMO and LUMO or the vertical I and A:

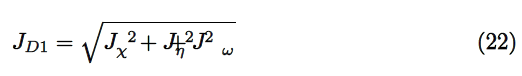
where D1 stands for the first group of Conceptual DFT descriptors.

Finally, we designed other four descriptors to verify the goodness of the studied density functionals for the prediction of the electroaccepting power ω⁺, the electrodonating power ω⁻, the net electrophilicity ∆ω^± , and for a combination of these Conceptual DFT descriptors, just considering the energies of the HOMO and LUMO or the vertical I and A:

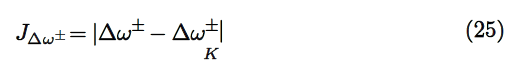
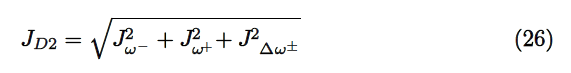
where D2 stands for the first group of Conceptual DFT descriptors.

The results of the calculations of J_I, J_A, J_Gap, J_χ, J_η, J_ω, J_D1, J_ω+, J_ω−,

J_∆ω± and J_D2 for the NHDC molecule are displayed in Table 2.

Table 2: Descriptors J_I, J_A, J_Gap, J_χ, J_η, J_ω, J_D1, J_ω+, J_ω−, J_∆ω± and J_D2 for the NHDC molecule calculated from the results of Table 1.

Atom M11 M11L MN12L MN12SX N12 N12SX SOGGA11 SOGGA11X

As can be seen from Tables 1 and 2, the ”Koopman’s theorem in DFT” holds with great accuracy for the MN12SX and N12SX density functionals, which are a range-separated hybrid meta-NGA and a range-separated hybrid NGA density functionals, respectively. Indeed, the values of J_I, J_A and J_Gap are not exactly zero. However, their values can be favorably compared with the results presented for these quantities in the work of Lima et al [22], where the minima has been obtained by chosing a parameter that enforces that behavior.

It is interesting to see that the same density functionals also fulfill the ”Koopmans’ theorem in DFT” for the other descriptors, namely J_χ, J_η, J_ω, and J_D1, as well as for J_ω−, J_ω+, J_∆ω±, and J_D2. These results are very important, because they show that it is not enough to rely only in J_I, J_A and J_Gap. For

example, if we consider only J_χ, for all of the density functionals considered, the values are very close to zero. As for the other descriptors, only the MN12SX and N12SX density functionals show this behavior. That means that the results for J_χ are due to a fortituous cancellation of errors.

The usual GGA (SOGGA11) and hybrid-GGA (SOGGA11X) are not good for the fulfillment of the ”Koopmans’ theorem in DFT”, and the same conclusion is valid for the local functionals M11L, MN12L and N12.

An important fact is that although the range-separated hybrid NGA and range-separated hybrid meta-NGA density functionals can be useful for the calculation of the Conceptual DFT descriptors, it is not the same for the rangeseparated hybrid GGA (M11) density functional. An inspection of Tables 1, 2 and 3 shows that this is due to the fact that this functional describes inadequately the energy of the LUMO, leading to negative values of A, which are in contradiction with the ∆SCF results.

The condensed Fukui functions can also be employed to determine the reactivity of each atom in the molecule. The corresponding condensed functions are given by f_k⁺ = q_k(N + 1) − q_k(N) (for nucleophilic attack), f_k⁻ = q_k(N)−q_k(N−1) (for electrophilic attack), and f_k⁰ = [q_k(N + 1) − q_k(N − 1)]/2 (for radical attack), where q_k is the gross charge of atom k in the molecule.

It is possible to evaluate condensed Fukui functions from single-points calculations directly, without resorting to additional calculations involving the systems with N-1 and N+1 electrons:

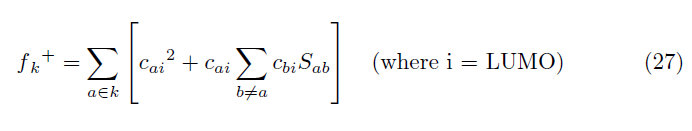
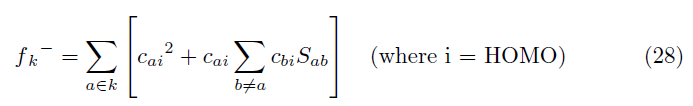
The condensed Fukui functions have been calculated using the AOMix molecular analysis program [51, 52] starting from single-point energy calculations.

The condensed dual descriptor has been defined as f⁽²⁾(r)_k = f⁺_k - f⁻_k [32, 33]. From the interpretation given to the Fukui function, one can note that the sign of the dual descriptor is very important to characterize the reactivity of a site within a molecule toward a nucleophilic or an electrophilic attack. That is, if f⁽²⁾(r)_k > 0, then the site is favored for a nucleophilic attack, whereas if f⁽²⁾(r)_k < 0, then the site may be favored for an electrophilic attack [32, 33, 53].

The condensed dual descriptor f⁽²⁾(r) over the atoms of the NHDC molecule calculated with the calculated with the MN12SX and N12SX density functionals and the Def2TZVP basis set using water as as solvent simulated with the SMD parametrization of the IEF-PCM model are shown in Table 3.

It can be concluded from the analysis of the results on Table 3 that both density functionals considered in this study predict that C34, that is, the carbonyl carbon atom will be the preferred site for a nucleophilic attack.

From the whole of the results presented in this contribution it has been clearly demonstrated that the sites of interaction, and hence, the chemical reactivity of the NHDC molecule can be predicted by using DFT-based reactivity descriptors such as the electronegativity, global hardness, global electrophilicity, electrodonating and electroaccepting powers, net electrophilicityy, as well as Fukui function and the condensed dual descriptor. These descriptors were used in the characterization and successfully description of the preferred reactive sites and provide a firm explanation for the reactivity of the NHDC molecule.

The Minnesota family of density functionals (M11, M11L, MN12L, MN12SX, N12, N12SX, SOGGA11 and SOGGA11X) have been tested for the fulfillment of the ”Koopmans’ theorem in DFT” by comparison of the HOMO- and LUMOderived values with those obtained through a ∆SCF procedure. It has been shown that the range-separated hybrid meta-NGA density functional ( MN12SX ) and the range-separated hybrid NGA density functional (N12SX) are the best for the accomplishment of this objective. As such, they are a good alternative to those density functionals whose behavior have been tuned through a gapfitting procedure and a good prospect for their usefulness in the description of the chemical reactivity of molecular systems of large size.

Table 3: Condensed dual descriptor f⁽²⁾(r) over the atoms of the NHDC molecule calculated with the MN12SX and N12SX density functionals and the Def2TZVP basis set using water as as solvent simulated with the SMD parametrization of the IEF-PCM model. The actual values have been multiplied by 100 for an easier comparison. H atoms are not shown.

This work has been partially supported by CIMAV, SC and Consejo Nacional de Ciencia y Tecnolog´ıa (CONACYT, Mexico) through Grant 219566/2014 for

Basic Science Research and Grant 265217/2016 for a Foreign Sabbatical Leave.

Daniel Glossman-Mitnik conducted this work while a Sabbatical Fellow at the University of the Balearic Islands from which support is gratefully acknowledged. This work was cofunded by the Ministerio de Econom´ıa y Competitividad (MINECO) and the

1. J.-M. Choi, B.-S. Yoon, S.-K. Lee, J.-K. Hwang, R. Ryang, Antioxidant Properties of Neohesperidin Dihydrochalcone: Inhibition of Hypochlorous Acid-Induced DNA Strand Breakage, Protein Degradation, and Cell Death, Biological & Pharmaceutical Bulletin 30 (2) (2007) 324?330. PMid:17268074

   View Article      PubMed/NCBI     

2. R. Parr, W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.

3. P. Geerlings, F. De Proft, W. Langenaeker, Conceptual Density Functional Theory, Chemical Reviews 103 (2003) 1793?1873. PMid:12744694

   View Article      PubMed/NCBI     

4. A. Toro-Labb?e (Ed.), Theoretical Aspects of Chemical Reactivity, Vol. 19, Elsevier Science, Amsterdam, 2007.

5. P. Chattaraj (Ed.), Chemical Reactivity Theory - A Density Functional View, CRC Press. Taylor & Francis Group, Boca Raton, 2009.

6. P. Politzer, J. Murray, The Fundamental Nature and Role of the Electrostatic Potential in Atoms and Molecules, Theoretical Chemistry Accounts 108 (2002) 134?142.

   View Article           

7. J. Murray, P. Politzer, The Electrostatic Potential: An Overview, WIREs Computational Molecular Science 1 (2011) 153?163.

   View Article           

8. S. Huzinaga, J. Andzelm, M. Klobukowski, E. Radzio-Audzelm, Y. Sakai, Tatewaki, Gaussian Basis Sets for Molecular Calculations, Elsevier, Amsterdam, 1984.

9. R. Easton, D. Giesen, A. Welch, C. Cramer, D. Truhlar, The MIDI! Basis Set for Quantum Mechanical Calculations of Molecular Geometries and Partial Charges, Theoretical Chemistry Accounts 93 (1996) 281?301.

   View Article           

10. E. Lewars, Computational Chemistry - Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Kluwer Academic Publishers, Dordrecht, 2003.

11. D. Young, Computational Chemistry - A Practical Guide for Applying Techniques to Real-World Problems, John Wiley & Sons, New York, 2001.

12. F. Jensen, Introduction to Computational Chemistry, 2nd Edition, John Wiley & Sons, Chichester, England, 2007.

13. C. Cramer, Essentials of Computational Chemistry - Theories and Models, 2nd Edition, John Wiley & Sons, Chichester, England, 2004.

14. L. Kronik, T. Stein, S. Refaely-Abramson, R. Baer, Excitation Gaps of Finite-Sized Systems from Optimally Tuned Range-Separated Hybrid Func- tionals, Journal of Chemical Theory and Computation 8 (5) (2012) 1515?1531. PMid:26593646

    View Article      PubMed/NCBI     

15. J. Perdew, R. Parr, M. Levy, J. LJ, Balduz, Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy, Physical Review Letters 49 (1982) 1691?1694.

    View Article           

16. C.-O. Almbladh, U. von Barth, Exact Results for the Charge and Spin Densities, Exchange-Correlation Potentials, and Density-Functional Eigenvalues, Physical Review B 31 (1985) 3231?3244.

    View Article           

17. J. Perdew, K. Burke, M. Ersernhof, Erratum: Generalized Gradient Approximation Made Simple, Physical Review Letters 78 (1997) 1396.

    View Article           

18. M. Levy, J. P. Perdew, V. Sahni, Exact Differential Equation for the Density and Ionization Energy of a Many-Particle System, Physical Review A 30 (1984) 2745?2748.

    View Article           

19. A. Savin, Beyond the Kohn - Sham Determinant, in: Recent Advances in Density Functional Methods, World Scientific, 2011, Ch. 4, pp. 129?153.

20. T. Leininger, H. Stoll, H.-J. Werner, A. Savin, Combining Long-Range Configuration Interaction with Short-Range Density Functionals, Chemical Pysics Letters 275 (3) (1997) 151?160. 00758-6

    View Article           

21. A. Savin, H.-J. Flad, Density Functionals for the Yukawa El????-ectron-Electron Interaction, International Journal of Quantum Chemistry 56 (4) (1995)327?332.

    View Article           

22. I. T. Lima, A. d. S. Prado, J. B. L. Martins, P. H. de Oliveira Neto, A. M. Ceschin, W. F. da Cunha, D. A. da Silva Filho, Improving the Description of the Optical Properties of Carotenoids by Tuning the Long-Range Corrected Functionals., The Journal of Physical Chemistry A 120 (27) (2016) 4944?4950. PMid:26885879

    View Article      PubMed/NCBI     

23. R. Peverati, D. G. Truhlar, Quest for a Universal Density Functional: The Accuracy of Density Functionals Across a Broad Spectrum of Databases in Chemistry and Physics., Philosophical Transactions. Series A, Mathematical, Physical, and Engineering Sciences 372 (2011) (2014) 20120476.

24. R. Parr, W. Yang, Density Functional Approach to the Frontier-Electron Theory of Chemical eactivity, Journal of the American Chemical Society 106 (1984) 4049?4050.

    View Article           

25. J. Janak, Proof that ?E/?ni = E in Density Functional Theory, Physical Review B 18 (1978) 7165?7168.

    View Article           

26. J. Zevallos, A. Toro-Labb?e, A Theoretical Analysis of the Kohn-Sham and Hartree-Fock Orbitals and their Use in the Determination of Electronic Properties, Journal of the Chilean Chemical Society 48 (2003) 39?47.

    View Article           

27. J. G?azquez, A. Cedillo, A. Vela, Electrodonating and Electroaccepting Powers, Journal of Physical Chemistry A 111 (10) (2007) 1966?1970. PMid:17305319

    View Article      PubMed/NCBI     

28. P. Chattaraj, A. Chakraborty, S. Giri, Net Electrophilicity, Journal of Physical Chemistry A 113 (37) (2009) 10068?10074. PMid:19702288

    View Article      PubMed/NCBI     

29. P. Ayers, The Dependence on and Continuity of the Energy and other Molecular Properties with respect to the number of Electrons, Journal of Mathematical Chemistry 43 (2008) 285?303.

    View Article           

30. P. Fuentealba, P. P?erez, R. Contreras, On the Condensed Fukui Function, Journal of Chemical Physics 113 (2000) 2544?2551.

    View Article           

31. F. Bulat, R. Chamorro, P. Fuentealba, A. Toro-Labb?e, Condensation of Frontier Molecular Orbital Fukui Functions, Journal of Physical Chemistry A 108 (2004) 342?349.

    View Article           

32. C. Morell, A. Grand, A. Toro-Labb?e, New Dual Descriptor for Chemical Reactivity, Journal of Physical Chemistry A 109 (2005) 205?212. PMid:16839107

    View Article      PubMed/NCBI     

33. C. Morell, A. Grand, A. Toro-Labb?e, Theoretical Support for Using the ?f (r) Descriptor, Chemical Physics Letters 425 (2006) 342?346.

    View Article           

34. C. C?ardenas, N. Rabi, P. Ayers, C. Morell, P. Jaramillo, P. Fuentealba, Chemical Reactivity Descriptors for Ambiphilic Reagents: Dual Descriptor, Local Hypersoftness, and Electrostatic Potential, Journal of Physical Chemistry A 113 (2009) 8660?8667. PMid:19580251

    View Article      PubMed/NCBI     

35. P. Ayers, C. Morell, F. De Proft, P. Geerlings, Understanding the Woodward-Hoffmann Rules by Using Changes in Electron Density, Chemistry - A European Journal 13 (2007) 8240?8247. PMid:17639522

    View Article      PubMed/NCBI     

36. C. Morell, P. Ayers, A. Grand, S. Guti?errez-Oliva, A. Toro-Labb?e, Ratio- nalization of the Diels-Alder Reactions through the Use of the Dual Reactivity Descriptor ?f (r), Physical Chemistry Chemical Physics 10 (2008) 7239?7246. PMid:19060968

    View Article      PubMed/NCBI     

37. C. Morell, A. Hocquet, A. Grand, B. Jamart-Gr?egoire, A Conceptual DFT Study of Hydrazino Peptides: Assessment of the Nucleophilicity of the Nitrogen Atoms by Means of the Dual Descriptor ?f (r), Journal of Molecular Structure:THEOCHEM 849 (2008) 46?51.

    View Article           

38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov,J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao,H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro,M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009.

39. F. Weigend, R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Physical Chemistry Chemical Physics 7 (2005) 3297?3305. PMid:16240044

    View Article      PubMed/NCBI     

40. F. Weigend, Accurate Coulomb-fitting Basis Sets for H to R, Physical Chemistry Chemical Physics 8 (2006) 1057?1065. PMid:16633586

    View Article      PubMed/NCBI     

41. R. Peverati, D. G. Truhlar, Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation, The Journal of Physical Chemistry Letters 2 (21) (2011) 2810?2817.

    View Article           

42. R. Peverati, D. G. Truhlar, M11-L: A Local Density Functional That Provides Improved Accuracy for Electronic Structure Calculations in Chemistry and Physics, TheJjournal of Physical Chemistry Letters 3 (1) (2012) 117?124.

    View Article           

43. R. Peverati, D. G. Truhlar, An Improved and Broadly Accurate Local Approximation to the Exchange-Correlation Density Functional: the MN12-L Functional for Electronic Structure Calculations in Chemistry and Physics, Physical Chemistry Chemical Physics 14 (38) (2012) 13171?13174. PMid:22910998

    View Article      PubMed/NCBI     

44. R. Peverati, D. G. Truhlar, Screened-Exchange Density Functionals with Broad Accuracy for Chemistry and Solid-State Physics, Physical Chemistry Chemical Physics 14 (47) (2012) 16187?16191. PMid:23132141

    View Article      PubMed/NCBI     

45. R. Peverati, D. G. Truhlar, Exchange-Correlation Functional with Good Accuracy for Both Structural and Energetic Properties while Depending Only on the Density and Its Gradient., Journal of Chemical Theory and Computation 8 (7) (2012) 2310?2319. PMid:26588964

    View Article      PubMed/NCBI     

46. R. Peverati, Y. Zhao, D. G. Truhlar, Generalized Gradient Approximation That Recovers the Second-Order Density-Gradient Expansion with Optimized Across-the-Board Performance, The Journal of Physical Chemistry Letters 2 (16) (2011) 1991?1997.

    View Article           

47. R. Peverati, D. G. Truhlar, Communication: A Global Hybrid Generalized Gradient Approximation to the Exchange-Correlation Functional That Satisfies the Second-Order Density-Gradient Constraint and Has Broad Applicability in Chemistry, The Journal of Chemical Physics 135 (19) (2011) 191102. PMid:22112059

    View Article      PubMed/NCBI     

48. A. Marenich, C. Cramer, D. Truhlar, Universal Solvation Model Based on Solute Electron Density and a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, Journal of Physical Chemistry B 113 (2009) 6378?6396. PMid:19366259

    View Article      PubMed/NCBI     

49. Avogadro: An Open-Source Molecular Builder and Visualization Tool - Version 1.2.0 - (2016).

    View Article           

50. M. Hanweel, C. D.E., D. Lonie, T. Vandermeersch, E. Zurek, G. Hutchison, Avogadro: An Advanced Semantic Chemical Editor, Visualization, and Analysis Platform, Journal of Cheminformatics 4 (2012) 17. PMid:22889332

    View Article      PubMed/NCBI     

51. S. Gorelsky, AOMix Program for Molecular Orbital Analysis - Version 6.5, university of Ottawa, Ottawa, Canada (2011).