L.K. Rogers-Bennett
E-mail: rogersbennett@ucdavis.edu
https://orcid.org/0000-0003-3309-5352
© 2019 Sift Desk Journals. All Rights Reserved
VOLUME: 5 ISSUE: 1
Page No: 543-549
L.K. Rogers-Bennett
E-mail: rogersbennett@ucdavis.edu
https://orcid.org/0000-0003-3309-5352
D.W. Rogers1, A.A. Zavitsas1, L.K. Rogers-Bennett2
1Department of Chemistry and Biochemistry, Long Island University, 1 University Plaza, Brooklyn, New York, USA 11201
2University of California, Davis, Bodega Marine Laboratory, 2099 Westside Rd, Bodega Bay, CA,
USA. 94923-0247
D.W. Rogers, Zavitsas, A.A. and L. Rogers-Bennett, HELICAL STRUCTURE OF POLYUNSATURATED FATTY ACIDS: GAUSSIAN G4 THERMODYNAMIC FUNCTIONS (2021) Journal of Computational Chemistry & Molecular Modeling 5(1):543-549
Molecular modeling of lipids has been hampered by the size of these complex, biologically important molecules. Yet, understanding the structure and energy (enthalpy) of large molecules is critical to identifying their function in chemical equilibrium and transition state theory. In this work, we use both experimental data and G4 computed results, to show that cis polyunsaturated lipids have helical conformers. We present linear functions for the enthalpy of formation ΔfH°298 and the Gibbs free energy of formation ΔfG°298 as a function of n, where n is the number of carbon atoms in a linear carboxylic acid chain. Taking ΔfH°298 of a saturated acid as a starting point, we add the enthalpy of hydrogenation ΔhydH°298 at appropriate locations on the carbon chain to model polyunsaturated fatty acids. For example, taking eicosanoic acid (C20) as a saturated starting point, we add four enthalpies of cis-dehydrogenation (ΔhydH°298) to obtain arachidonic acid (eicosa-5Z,8Z,11Z,14Z-tetraenoic acid). We compare Gaussian-4 computational results, to show evidence of helical structure. We conclude that fatty acids can have helical conformers facilitating a broad range of biological functions.
Keywords: G4 Calculations, Helix, Lipid, Molecular Structure, Thermochemistry
Fatty acids are key compounds in plant and animal nutrition, serving as molecular energy storage units, signaling compounds, and essential components of cell membranes. Animals can synthesize some fatty acids, but others (called essential) fatty acids can not be synthesized by the animal and must be ingested for normal growth. Biologically active fatty acid derivatives have been found in all animal tissues and have hormone-like signaling functions [1] which depend on their structure. Polyunsaturated fatty acids (PUFA) have more than one double bond in their “backbone“. Fatty acids with double bonds in the 9 and 12 positions fall in the linoleic acid group and those with double bonds in the 9, 12, and 15 positions are in the linolenic group. Arachidonic acid, eicosa-5Z,8Z,11Z,14Z-tetraenoic acid, is a precursor to a remarkable group of bioactive eicosenoids including anticonvulsants, anti-inflamatory lipoxins, and the seemingly contradictory vasoconstrictors and vasodilators [2, 3]. It is known that binding proteins have helical strucures that bind single molecule long chain fatty acids such as intestinal fatty acids [4]. Starches as well have long been known to have helical structures [5]. Law et al have studied the structure of some of the higher fatty acids, along with fatty acid influence on the thermochemistry of folding of polyallylic hydrocarbons, and anticipated fatty acid use in the study of protein folding [6, 7].
Until recently, determination of the molecular structure and thermodynamic parameters of PUFA and their derivatives has been limited by the complexity and size of the molecules, coupled with limited computer speed and memory. The advent of supercomputers equipped with multiple integrated processor clusters has increased the speed of computing beyond 2 petaFLOPS (2 × 1015 FLoating point Operations Per Second). It is now possible to run a series of ab initio molecular orbital calculations and to arrive at structural parameters which successfully model biophysically important lipids. Modern hardware and software are capable of determining the total energy and enthalpy of fatty acids with CH2 chains up to 11 carbon atoms in a reasonable amount of computing time. With 24 processors and sufficient memory storage (248 gigabytes = 2.48 × 1011 bytes) and armed with a system for calculating self-consistent enthalpies of formation and Gibbs free energies of formation ΔfH°298 and ΔfG°298 at 298 K of relatively large component parts of a fatty acid molecule, we can obtain reliable component sums on the principle that the whole is the sum of its parts.
We have computed the structure and enthalpy of formation of nonane, pentanoic acid, and hexane, the sum of which is the enthalpy of formation of eicosanoic acid, CH3(CH2)18COOH
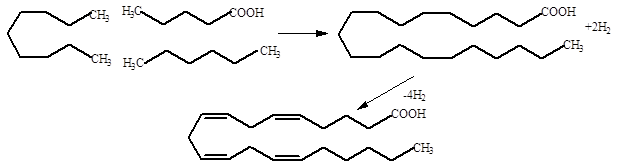 (1)
(1)
Dehydrogenation of eicosanoic acid to find ΔfH°298 of eicosatetraenoic acid, as shown above, leads to a dehydrogenation enthalpy of 480 kJ mol-1
ΔfHo298 = ΔfHo298 (intercept) + n(ΔfH°298) = -812.4 kJ mol-1 + 4(120.0) kJ mol-1
ΔfHo298 (eicosanoic acid) + n(ΔhydH°298) = -812.4 + 480.0 = -332.4 kJ mol-1 (2)
EXPERIMENTAL
2.1. Theory
Ethene H2C= CH2 is planar. When two simple ethene molecular components are linked to each other through a methylene carbon –CH2–, the result is penta-1,4-diene, CH2=CH-CH2-CH=CH2. Electron repulsion causes the planar ethene groups to be oriented at a maximum distance from one another consistent with the tetrahedral distribution of bonding electrons in the methylene carbon atom. Free rotation at the –CH2– bond results in a dihedral angle of approximately 120°.
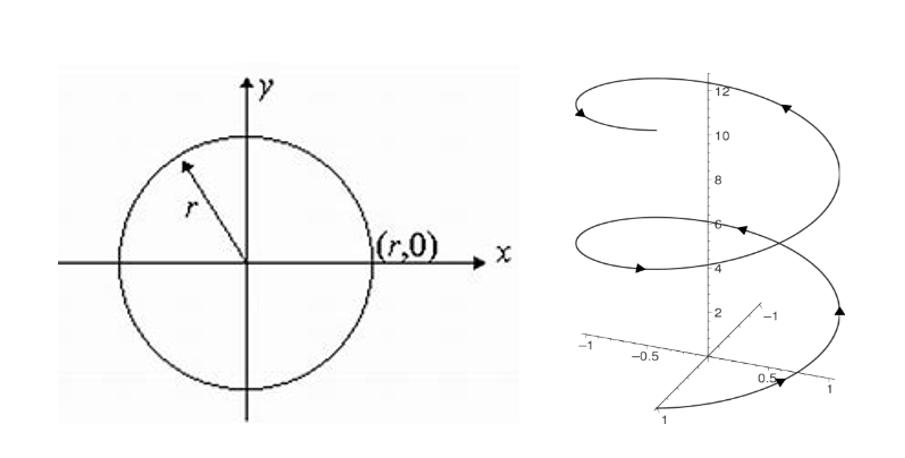
Figure 1. If a radius vector is rotated in a plane, the resulting trace is a circle. If the base of the plane is raised at a constant rate during rotation, the resulting trace is a helix.
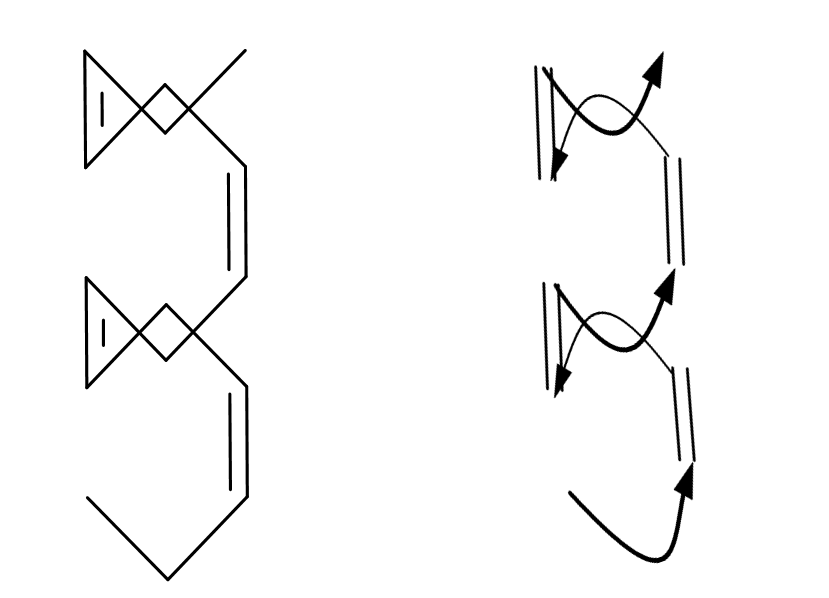
Figure 2. Pentadeca-3,6,9,12-tetraene is shown from two different angles. The view at right above shows the a helical form for this simple molecule. The heavier curved lines represent a -CH2 - linkage under the page.
2.2. Method
Preliminary energy minimization of an input geometry was carrried out using procedures MM3 or MMX, which are included in the molecular structure software [8]. Full structure and enthalpy calculations were then carried out using the Gaussian G4 composite quantum chemical method based on a sequence of single point energy calculations. The composite program includes an extrapolation to the Hartree-Fock limit for the first step in the energy calculation. A high-level calculation using a coupled cluster (CCSD)(T) correlation treatment with a relatively small basis set, followed by a lower-level calculation (MP2 or MP4) carried out with a larger basis set. The optimized geometry and zero-point energy are obtained at the B3LYP level followed by combination of the result with a set of small low-level empirical corrections (HLC) to arrive at an accurate value for the structure, enthalpy of formation, and related energy values [9, 10].
In some cases, these new computed values confirm existing experimental results and in others, they do not. We replace erroneous experimental results or call attention to input files that seem to be in substantial error. Extensive comparison with existing experimental results has been carried out [10, 11, 12]. Over one test set (454 energies), the deviation from experiment is less than 4 kJ mol-1. The method has been described in more detail elsewhere [10].
Once having found the Gaussian-4 G4 enthalpy of formation at 298 K of an alkanoic acid, the value is readily converted from the G4 atomic standard state of elementary particles to the more familiar molecular standard state H2(g), O2(g) and C(solid), all at 298 K and 1 bar [12]. The conversion can be for an alkanoic acid, a singly unsaturated acid or for multiply unsaturated alkenoic acids according to the number of double bonds in the target molecule. By addition of ΔhydH°298 = 124.4 kJ mol-1 for the appropriate number of cis double bonds, one has ΔfH°298 of the selected alkenoic acid. Gibbs free energies of formation ΔfG° are treated in the same way. For trans double bonds the ΔhydH°298 value is 120.2 kJ mol-1 [13, 14].
For long-chain PUFA, ΔfH° was extrapolated to C20 or C22 to obtain ΔfHo298 estimates of the G4 results. Being essentially repetitive calculations with an increase in the parameter n, there is no appreciable scatter about the linear function, the only question is the accuracy of the slope over such a long extrapolation. A few reliable points have been found in the literature for verification of the G4 slope and intercept of longer alkanoic chains (Table 1.).
Determining the molecular structure and thermodynamic parameters of PUFAS and their derivatives is challenging for both the experimentalist and the theoretical chemist due to the complexity and sheer size of the target molecules. We found that results from Gaussian-4 calculations with carbon numbers C4 to C11 can be compared to experimental results with satisfactory agreement but that results for C12 to C22 can not because reliable experimental values are not available. The point of the present work is to model the thermochemical parameters of the higher linear saturated, unsaturated, or polyunsaturated acids, including arachidonic acid, docosapentaenoic acid, and eicosapentaeneoic acid (EPA) [19].
Values we obtained for Gaussian-4 enthalpies of formation ΔfHo298 in units of hartrees for a series C4 to C11 saturated fatty acids closely follow the linear equation for ΔfHo298 in units of hartrees.
ΔfHo298 [stearic acid]= -762.7 kJ mol-1 (eq.1)
where b is the intercept of the function, k is the slope, and n is the number of carbons. The function was optimized by a simple linear least squares procedure [11]. Values of ΔfHo298 for n = 2, 3, and 11 were omitted from the chain-length curve fit to avoid interference by resonance with the COOH group at one end and the “terminal effect“ (CH2–CH3 interactions) at the other. When C2, C3, and C11 carbon atoms were included in the calculation, there was no significant difference in the calculated slope and intercept.
The experimental enthalpy of hydrogenation ΔhydHo of the cis double bond in oleic (cis-9-octadecenoic) is –124.4 ± 1.2 kJ mol-1 [12] so, reversing the sign, we added the increase in enthalpy to the linear function ΔfHo298 of stearic acid (-781.2 +124.4 to obtain - 656.8 kJ mol-1)
ΔfHo298 [oleic acid] = –762.7 + 124.4 = –638.6 kJ mol-1 (exper: -661.2 kJ mol-1) (eq.2)
Please note that the added 124.4 ± 1 is an enthalpy of dehydrogenation. When stearic acid has been dehydrogenated, we have moved from the saturated acid to the 9Z unsaturated octadecenoic acid also called oleic acid. The 9E isomer is called elaidic acid and its experimental ΔhydHo is –120.2 ± 2.0 kJ mol-1.
Continuing the extrapolation procedure from C18 to C20 (eicosanoic acid); a Gaussian-4 estimate of the enthalpy of formation of eicosanoic acid, followed by 4 dehydrogenation enthalpies of ΔhydHo298 = –124.4 kJ mol-1 leads to the enthalpy of formation of arachidonic acid
ΔfHo298 [arachidonic acid]=-804.5 + 4(124.4) = –306.9 kJ mol-1 (eq.3)
which is higher in the potential enthalpy well than eicosapentaenoic acid, or EPA, by 124.4 kJ mol-1, leading to the result
ΔfHo298 [eicosapentaenoic acid] = -804.5 + 5(124.4) = –182.5 kJ mol-1 (eq.4)
Table 1 provides a summary of applications of the above precedures for several important polyunsaturated fatty acids.
Experimental enthalpies of dehydrogenation, of unconjugated cis double bonds in a long chain have consistent values of 118 to 122 kJ mol-1 approximately 120.4. Therefore, an extrapolated value of stearic acid leads to
ΔfH°298 (stearic acid) + ΔdehydH°298 = ΔfH°298 (oleic acid),
ΔfH°298 (oleic acid) + 120.0 kJ mol-1 = -781.2 + 120.0 = -661.2 kJ mol-1
ΔfH°298 (linoleic acid) + 2(-120.0) kJ mol-1 = -781.2 + 240.0 = -541.2 kJ mol-1
ΔfH°298 (arachidonic acid) + 4(-120.0) kJ mol-1 = -781.2 + 480.0 = -301.2 kJ mol-1
Table 1. Estimated enthalpies of formation of polyunsaturated fatty acids. Temperatures are 298 K. Experimental uncertainties are approximate.
|
Acid |
Formula |
ΔfHo298 Exper. |
ΔhydHo (12) |
ΔfHo298 |
|
Stearic |
C18H36O2 |
–781.2 ± 4.7 |
0 |
–762.7 |
|
Oleic (Z) |
C18H34O2 (Z) |
–656.8 ± 6 |
–124.4 ± 1.2 |
–638.6 |
|
Elaidic (E) |
C18H34O2 (E) |
–120.2 ± 2.0 |
–642.5 |
|
|
Linoleic (ZZ) |
C18H32O2 (ZZ) |
–248.8 ± 1.5 |
–513.9 |
|
|
Linoelaidic(EE) |
C18H32O2 (EE) |
–240.4 ± 2.5 |
–522.3 |
|
|
Linolenic(ZZZ) |
C18H32O2 (ZZZ) |
–373.2 ± 1.9 |
–389.5 |
|
|
Eicosanoic |
C20H40O2 |
–812.4 ± 7.7 |
0 |
–804.5 |
|
Arachidonic |
C20H32O2(ZZZZ) |
–314.8 ± 9 |
–301.2 ± 2.2 |
–306.9 |
It has long been known that PUFAs have a linear sequence of double bonds making them reactive, but until now the helix structure has not been explicitly modeled. We model the structure of long chain PUFA (>12 chain carbons) by adding the G4 enthalpies of dehydrogenation to the corresponding saturated acids thereby raising ΔfHo298. We have found that the –CH2– units may form helices according to their (presumably) random orientation with one another. The structure of these long chain molecules can now be determined due to advances in both computational capabilities and computational molecular modeling software [10, 15, 16]. A body of work has been built determining the structures of short chain molecules [17, 18, 20, 21]. Many of these PUFA compounds have potent physiological properties tied to intra- and extra-cellular messengers whose mechanisms of action are poorly understood. The envisioning of PUFA structures presented here will enable new insights into the function of these molecules, related to thermochemistry, equilibration chemistry, kinetics, structure, and bending at the double bonds [6, 11].
Gaussian-4 (G4) computations [10] of the enthalpies of formation of alkanoic acids has shown that insertion of one or more CH2 groups into the saturated chain increases its enthalpy of formation by precisely -39.27691 EH kJ mol- [11]. Thus, a plausible extrapolation can be carried out using a linear function fitted to known experimental values of ΔfH°298 for acids (< C11) to estimate ΔfH°298 values of long-chain alkanoic acids, [11] which are at present scattered. Having extrapolated the Gaussian-4 function to the enthalpy of formation of a long-chain saturated acid[13], one may then add one or more enthalpies of hydrogenation ±ΔhydH°298 to obtain ΔfH°298 of the corresponding unsaturated acid. Notice that ΔdehydH°298 is a positive enthalpy of dehydrogenation.
The number of carbon atoms is not changed by this. One or more pairs of carbon atoms are selected and two H atoms are withdrawn from each pair by the dehydrogenation operation, leaving one or more unconjugated cis ethene groups, –CH=CH– in the molecule. Common biologically important acids like arachidonic acid and eicosapentaenoic acid [eicosa-5Z,8Z,11Z,14Z,17Z-pentaenoic acids, also called eicosa-3Z,6Z,9Z,12Z,15Z-pentaenoic acid or EPA] are examples in which a helical conformer is expected.
The number of conformers in a methylene connected polyene goes up as 2n where n = 0, 1, 2, 3, … is the number of dihedral angles. Four or five cis oriented, methylene-interrupted double bonds are found in some common polyunsaturated fatty acids. Figure 3 shows an omega-3-polyunsaturated fatty acid. The actual molecule is too large for a complete G4 calculation with present computational hardware and software but the acid can be modeled by inserting a computed structure of 5 methylene-connected, cis ethene groups into the 3 position of butanoic acid.
The model is then subject to preliminary optimization by MM4. This pre-insertion optimization was used to reduce compute time and memory demands. Numbers designating the carbon atoms are counted from the left in this figure. Following chemical convention, the carbons would be counted from the carboxyl group to find ω3-eicosa-5Z,8Z,11Z,14Z,17Z-pentaenoic acid. The G4 estimate of the length of the unsaturated portion of EPA is modeled by eicosa-2Z,6Z,9Z,11Z,14Z-pentaene. The eicosapentaene helix is 12.5 Å long and has a radius of about 4 Å.
This helical structure is more compact and stable than a chain conformation which has important implications for biological function. Based on historical as well as theoretical grounds, many properties of a (large) molecule can be seen as the sum of its parts [20, 22, 23]. Using this method, we find that the PUFA may have helical conformers. We see in the example of eicosapentaene, the helical portion of eicosa-2Z,6Z,9Z,11Z,14Z-pentaene has a radius = 4.0 Å and length = 12.5 Å. The helical conformer of lipids may be related to the messenger function in lipids and allows for compact packaging. The helical structure of proteins for example DNA have been known for decades however little work until now has been directed to the study of helical conformers in fatty acids.
Competing Interests
The authors declare no financial or non-financial competing interests.
Funding
We wish to acknowledge support of this project, by the National Science Foundation CHE 120084 (Renewal) by XRAC, of the San Diego Supercomputer Center, Dell Cluster computer (Comet) and disk storage (Data Oasis)resources as well as the Comet computer scientists at UC San Diego for their support.
Acknowledgements
We salute the memory of Dr. N.L. Allinger for his ground breaking work in the field of molecular struc-ture and we thank Kevin Gilbert of Serena Software. We thank the Whiteley Center, Friday Harbor Labs, University of Washington for intellectual exchange of ideas about marine lipids and space to think. We thank Long Island University for technical support, the University of Washington for similar support, and the Whiteley Foundation for a Whiteley Fellowship during which part of this work was carried out.
S.Tara, The Secret Life of Fat, Norton & Co Inc, NY, 2017.
M.M. Martínez, Mougan, I. Fatty acid composition of human brain phospholipids during normal gestation The Journal of Neurochemistry 1998, 71, 2528-2533. PMid:9832152
View Article PubMed/NCBIG.D. Lawrence, The Fats of Life. Essential Fatty Acids in Health and Disease Rutgers University Press, New Brunswick, NJ. 2010.
View ArticleR.A. Steele, D.A. Emmert, J. Koa, M.E. Hodsdon, C. Frieden, D.P. Cistola. The three-dimentional structure of a helix-less variant of intestinal fatty acid-binding protein. Protein Science 1998, 7, 1332-1339. PMid:9655337
View Article PubMed/NCBIF. Mikus, R. Hixon, R. Rundle The complexes of fatty acids with amylose. J. Am. Chem. Soc., 1946, 68, 1115-1123 PMid:20985626
View Article PubMed/NCBILaw J.M.S. Setiadi, D.H. Chass, G.A. Ciszmadia, I.G. & Viskolcz, B. Flexibility of Polyunsaturated Fatty Acid chains and Peptide Backbones: Comparative ab Initio Study J Phys Chem A 2005, 109, 520-533. PMid:16833374
View Article PubMed/NCBILaw J.M.S. Szori, M. Izska, R. Ciszmadia, I.G. Penke B, Folded and Unfolded Conformations of the ω-3-Polyunsaturated Fatty Acid Family: CH3CH2[CH=CHCH2]B-[CH2]-MCOOH: First Principles Study J Phys Chem A 2006, 110, 6100 - 6111. PMid:16671681
View Article PubMed/NCBIGilbert K. Serena Software, 3445, NW, 221st Ter, Hillsboro, OR, USA 97123
Curtiss L.A. Redfern, P.C. & Raghavachari, K. Gn Theory, Advanced Review WIREs Comput Mol Sci 2011, 1, 810-825. DOI: 10.1002/wcms.59.
View ArticleH. Hart, D.J. Hart, L.E. Craine, Organic Chemistry, A Short Course, 9th Ed. Houghton Mifflin Co., Princeton, NJ. 1995.
D.W. Rogers, A.A. Zavitsas, Enthalpies of reaction, formation, and hydrogenation among terminal and interior long chain alkanes, monoalkenes, acids, alcohols, and amines: G4 computed and experimental results, J Chem Thermodyn 2015, 79, 258-265.
View ArticleS. Rayne, K. Forest, Estimated gas-phase standard state enthalpies of formation for organic compounds using the Gaussian-4 (G4) and W1BD theoretical methods, Journal of Chemical Engineering Data 2010, 55, 5359 - 5364.
View ArticleD.W. Rogers, D.W., O.P.A. Hoyte, R.K.C. Ho. Hydrogenation of Large Molecules: Part 2. Six unsaturated and polyunsaturated fatty acids. J. Chem. Soc., Faraday Trans. 1: Physical Chemistry in Condensed Phases 1978, 74, 46-52.
View ArticleD. W Rogers, Heats of Hydrogenation, World Pub Co, 27 Warren St. 401-402, Hackensack, NJ, 2006.
Curtiss L.A. Redfern, L. A. & Raghavachari, K. Gaussian 4 theory. J Chem Phys 2007, 126, 084108. PMid:17343441
View Article PubMed/NCBIN.L. Allinger, Molecular Structure: Understanding Steric and Electronic Effects from Molecular Structure, John Wiley & Sons 110 River St., Hoboken, NJ. 2010.
View ArticleH,Y. Afeefy, J.F. Liebman, & Stein S.E. Neutral Thermochemical Data, in: NIST Chemistry Webbook, NIST Standard reference database number 69. P. J. Linstrom, W. G. Mallard Eds. National Institute of Standards and Technology, Gaithersburg, MD. 2009.
A.A. Zavitsas D.W. Rogers N. Matsunaga (2011) Destabilization of conjugated systems of Dicarbonyls and of Cyanogen, Australian Journal of Chemistry 2011, 64, 390 - 393.(2011).
View ArticleWikipedia Retrieved March 31 2021.
View ArticleD.W. Rogers, A.A. Zavitsas, Using only the very accurately known experimental enthalpy of formation of ethene as a reference standard in the atomization method. Structural Chemistry 2013, 24, 1909-1921.
View ArticleD.W. Rogers, A.A. Zavitsas, L.K. Rogers-Bennett, The Gaussian G4 structure, enthalpy, and free energy of formation of trans-dimethyl-, diethyl, dipropyl-, and dibutylcyclopentanes. J. Mol. Model. 2019, 25,233 PMid:31327068
View Article PubMed/NCBIForesman, J. B.; Frisch, A. Exploring Chemistry With Electronic Structure Methods: A Guide to Using Gaussian. 2nd Edition Gaussian Inc. MA. 1996.
Mc Quarrie D A, Simon J D, Molecular Thermodynamics, University Science Books, Sausalito CA 94965. 1999.
