Modeling a HPGe detector's absolute efficiency as a function of gamma energy and soil density in uncontaminated soil

Maurice O. Miller, PhD

Department of Physics, University of the West Indies, Mona Campus, Kingston, Jamaica

Email: moneilmiller@gmail.com

Maurice Oneil Miller, Modeling a HPGe detector's absolute efficiency as a function of gamma energy and soil density in uncontaminated soil(2018)SDRP Journal of Earth Sciences & Environmental Studies 3(4)

This study develops a mathematical model for predicting the absolute efficiency value of a HPGe detector based on the gamma energy and soil density for a typical counting arrangement for measuring gamma activity concentration in uncontaminated surface soils. The generation of the experimental efficiency curves was carried in AGLE 3.0 using the Ortec GEM-FX8530P4 with a warranted resolution (FWHM) at 1.33 MeV (Co-60) =1.9 keV and factory reported measured value of 1.76 keV. ANGLE 3.0 was used to output the efficiency and solid angle data for the various soil densities in the density range 0.8 – 1.8 g cm^-3 and gamma range 20 – 2000 keV. The inter-relationship is defined using SigmaPlot, as a 3D Lorentzian model with R²= 0.9925. Further analysis was done to determine the uncertainties in this predictive model, and a set of correcting equations based on energy ranges were developed. The data indicated that with each soil density, the uncertainties increase with increasing gamma energy in the energy range 400 – 1600 keV, and that the level of uncertainty was significant. The uncertainties at the energy range below 400 keV were not considered significant within the context of general experimental errors.

Keywords: detector characterization, semi-empirical, ANGLE, uncertainties, HPGe, detector efficiency

In determining the activity of gamma emitters with HPGe detectors, it is routine to compare measurements of an unknown source with those of a calibrated source of equivalent geometry and density. The total efficiency is defined as the ratio of the number of pulses recoded in the spectrum and the number of photons emitted by the source. Detector full-energy efficiency curves form the foundation on which accurate radioactivity is measured in environmental samples such as top soil using a standard and verifiable source counted above the detector. The specific activity (A) of the sample is measured by the formula shown below:

Equation 1 - Measurement of the specific activity

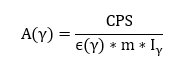
where CPS = net count per second under the gamma peak of interest; = branching ratio, m = mass, and ε(γ) = absolute or full energy peak efficiency for a particular gamma energy of interest. From equation 1, it is apparent that any over-statement or understatement of the efficiency value leads to an under-statement or overstatement respectively of the radioactivity of the sample. Typically the uncertainty in the efficiency calibration is the largest contributor to the total uncertainty in the measurement [1]. ANGLE uses the concept of the effective solid angle (Ω) to calculate the value of the energy dependent full-energy peak efficiency or absolute efficiency qualitatively defined in Equation 2.

Equation 2 - Full-energy peak efficiency

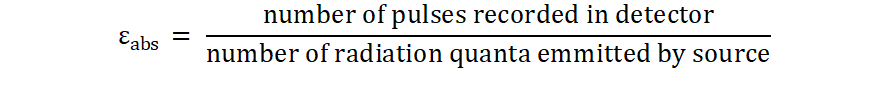
This efficiency is impacted by the detector properties and the solid angle (Ω) subtended by the radioactive source counted on the face of the detector. The absolute efficiency of the sample  is related to that of the reference standard ε_abs,ref  by the expression in Equation 3 [2].

Equation 3 - Efficiency and solid angle relationship

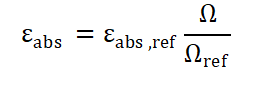
The key is the determination of ε, which may be experimentally determined by fitting a function of the form shown in Equation 4 to a plot of full-energy efficiency versus gamma energies using a reference source of verifiable activity and reference date to account for activity on the date of measurement. Various software can be used to determine the efficiency fitting parameters “a, b, c and d” below, which can then be extrapolated to determine the gamma energies of interest. SigmaPlot version 10 was used in this research due to its ease of use and flexibility.

Equation 4 - Absolute Efficiency

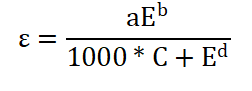
The absolute efficiency  is a function of the solid angle Ω; the solid angle is dependent on the source to detector distance or counting geometry. In this paper, the geometry employed is an Eu 152/154 cylindrical and disc calibration sources; the former in contact geometry with the detector and the latter counted 25 cm above the face of the detector.

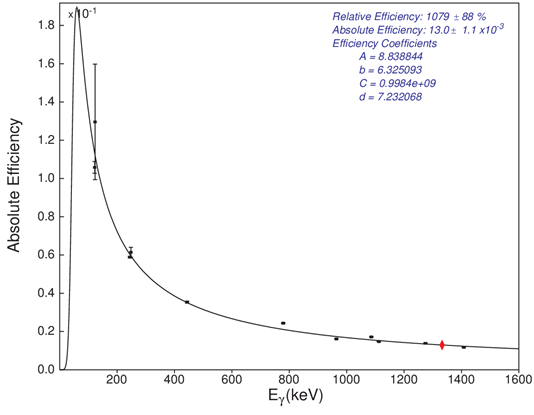
Figure 1: Absolute efficiency curve for the  Eu-152(93%) – Eu-154(7%) source in a cylindrical container of volume 63 cubic cm  and activity 6.7 +/- 0.2 kBq (as of 20/2/2001) and in touch geometry with the HPGe detector. Efficiency results corrected for energy drift and summing effect by SPECTRA software

The empirical function used for the fit is shown in Equation 5

Equation 5 - The empirical function used for the fit:

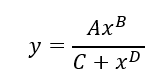
where A = 8.838844, B = 6.325093, C = 0.998e + 09, and D = 7.232068, x = gamma ray energy and y = absolute efficiency.

Numerous studies to optimize detector efficiency have been conducted for point and extended sources using Monte Carlo and optimization of geometric parameters for Marinelli beakers [3-7]. Monte Carlo determination of water concentration effect on gamma-ray detection efficiency in soil samples for photon energies ranging from 60 keV to 2 MeV developed corresponding correction factors. It this study, it was observed that the correction factor approaches unity with increasing energy and decreases with increasing water concentration [8]. The impact of soil density on in situ gamma spectra analysis has been studied to determine the specific relationship between soil bulk density and peak-to-valley ratio of natural radionuclides [9]. The impact of material density on gamma attenuation has been established in a number of studies [9-13]. Finally, a review and application of computer codes to develop absolute full-energy peak efficiency at the desired gamma-ray energy has been undertaken [14, 15].

The objective of this study is to develop a mathematical model for predicting the efficiency value of the soil’s primordial gamma ray based on its density and the energy of the emitted gamma. The counting geometry employed is the typical plastic cylindrical container in contact geometry with the face of a HPGe detector.

The generation of the experimental efficiency curves was carried using the Ortec GEM-FX8530P4 with a warranted resolution (FWHM) at 1.33 MeV (Co-60) = 1.9 keV and factory reported measured value of 1.76 keV. The amplifier shaping time was 6μs, peak-to-Compton ratio (Co-60) was 55:1 (warranted) and 61:1 measured, relative efficiency at 1.33MeV (Co-60) was 40.5 %. The setup consisted of a high voltage filter, detector, and pre-amplifier all housed in the detector casing. A recommended high voltage of 4800V was applied to the detector from a FAST NHQ-205M NIM module. [16]. The dimensions of the cylindrical container used for the soil and EU-152/154 efficiency measurements were as follows; diameter = 70mm, height = 21mm, bottom thickness = 1mm, and side thickness = 1mm. Details of the preparation of the Eu-152/154 calibration sources used in this paper have been published [17]. Figure 1 shows the detector’s configuration as supplied by the manufacturer, ORTEC. In ANGLE, the input data are categorized as detector, container, geometry, source and reference efficiency curve. The majority of the data requirement is for the detector. Details of the input to ANGLE are available on Ortec’s help documentation [18] .

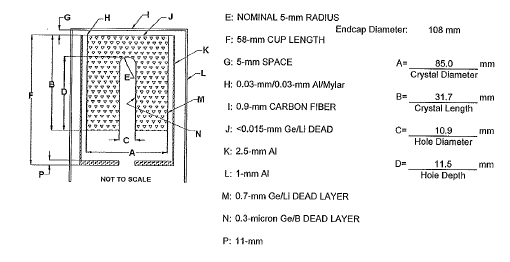
Figure 2: Detector parameters for GEM-FX8530P4 HPGe detector. Data courtesy of Ortec.

ANGLE 3.0 was used to output the efficiency and solid angle data for the various soil densities in the density range 0.8 – 1.8 g cm^-3 and gamma range 20 – 2000 keV. The density range was selected based on 66 soil samples collected island-wide in Jamaica, and the gamma energy range covers the main primordial gamma energies for environmental sample analysis. The data was input to SigmaPlot software which was used to generate the 3-D plot shown in Figure 2 and the mathematical description of the formula show in the Results and Discussion section of this paper.

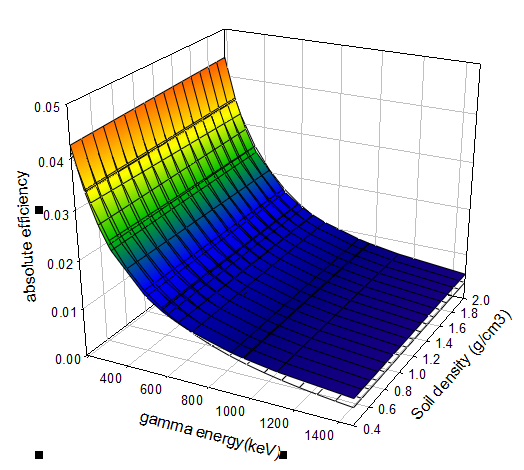
Figure 3: Predicted gamma efficiency as a function of soil density and gamma energy

Figure 3 shows plot a of the gamma efficiency value versus gamma energy as a function of soil density, for the counting geometry established in this study. A mathematical model for describing this curve is shown in Equation 6.

Equation 6 - 3D Lorentzian model for soil density, gamma energy and efficiency

ɛ=A/((1+((ρ-X₀)/B)^2)*(1+((γ-Y₀)/C)^2))

ɛ, ρ and γ denotes the efficiency values, soil density and gamma energy respectively, with X₀ = -263.6587, Y₀ = -0.5757, A = 0.1674, B = 257.9514, and C = 15603.6766. The quality of the fit is described with R²= 0.9927 with standard error of estimate = 0.0010. Sigma Plot reported the Total Number of Fits = 400 and Maximum Number of Iterations =200. The Kolmogorov-Smirnov goodness-of-fit test for the data set indicated a statistic = 0.1442 and significance level = <0.0001 which indicated that which rejected the hypothesis that the distribution differed substantially from theoretical expectations.

In Figure 4, the lowest end of the soil density was used to compare the actual versus predicted (fitted value) for the absolute efficiency over the range 200 – 1660 keV. The black dots represent  the actual values and the white dots represent the predicted values for the absolute efficiency. The fitted curve developed was an exponential decay, double, 4-parameter curve as shown in Equation 7.

Equation 7 - The actual versus predicted (fitted value, ) for the absolute efficiency over the range 20 – 1660 keV for soil density = 0.4 g/cm³

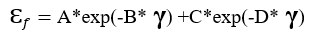
with the following denotations; f = fitted value of the efficiency, γ = gamma energy, A = 0.0851, B = 0.0060, C = 0.0185, and D = 0.0009.

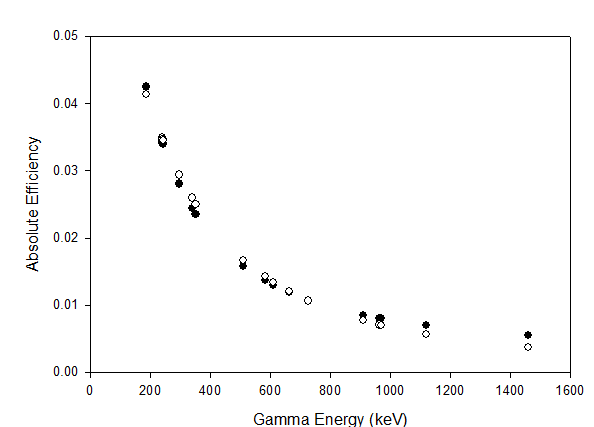
Figure 4: Predicted versus actual gamma efficiency for soil density = 0.4 g/cm³

Further analysis was done to determine the uncertainties in this predictive model, and to develop necessary correcting equation. Figures 5 and 6 shows the percentage errors in the energy range 20-400 keV and 400 – 1600 keV respectively.

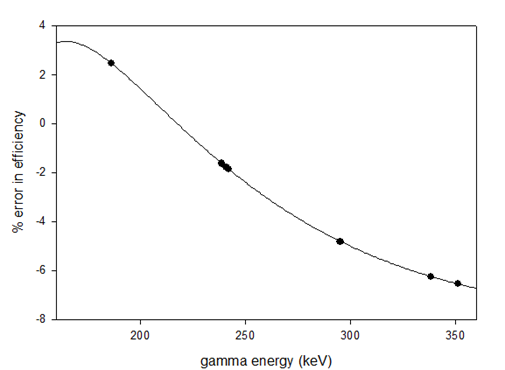
Figure 5: Percentage error in efficiency for the energy range between 0 to 400 keV

The fitting curve for Figure 4 is described by the polynomial, inverse third order equation shown in Equation 8:

Equation 8 - Percentage error in efficiency for the energy range between 0 to 400 keV

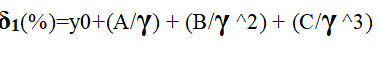
where δ₁(%)= percentage error in the efficiency value, y0 = 3.2390, A = -12229.4007, B = 4033136.9472, C =, -331978265.5734, and γ = gamma energy. The quality of the fit is denoted by a R² = 1.0000, which suggest a perfect fit for all points in the designated region. The findings show that within the 0 – 400 keV range, the error in the efficiency values decrease with increasing gamma energies. The error values fall within the -7% - 3% range and may therefore be ignored within the context of general experimental errors.

From Figure 5 (energy > 400keV), the fitting curve is a polynomial, quadratic equation shown in Equation 9.

Equation 9 - Percentage error in efficiency for the energy range 400 keV to 1600 keV

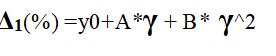
where Δ₁(%) = percentage error in the efficiency value, y0 = -26.8198, A = 0.0371,  B = 2.9059E-006, and γ = gamma energy. The quality of the fit is denoted by a R² = 0.9993, which suggest a good fit for all points in the designated region. The findings show that within the 400 – 1600 keV range, the error in the efficiency values increases with increasing gamma energies. Unlike the previous energy range, the error values fall within a wider range of -10% - 30% range, and therefore cannot be ignored. Equation 9 is then used to correct for the errors inherent in the Lorentzian model shown in Equation 3.

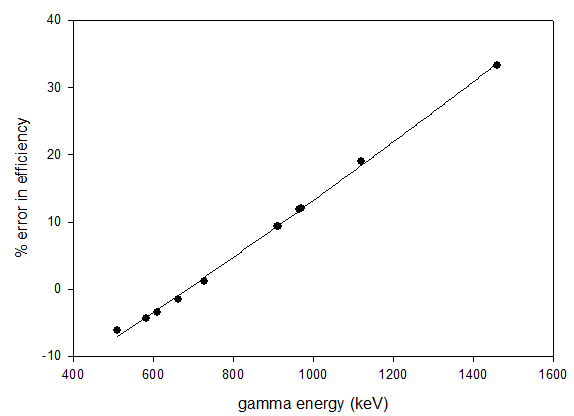
Figure 6 : Percentage error in efficiency for the energy range between 400 to 1600 keV

The final model based on corrections to the energy efficiency is show in Equation 10.

Equation 10 - Improved predictive model incorporating error corrections

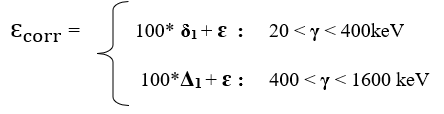
where  and ɛ, represents the corrected efficiency value and uncorrected efficiency value (defined in Equation 6) respectively, and δ₁ and Δ₁ are the correcting functions defined in Equations 8 and 9 for the energy intervals 20 – 400 keV, and 400 – 1600 keV respectively.

A mathematical model using commercially available software tools was developed and tested to produce the absolute efficiency values for an HPGe detector in a typical counting arrangement for uncontaminated soils. To reduce errors in the model, the necessary correcting equations were developed to improve the reliability of the efficiency values. The analysis of errors in the efficiency values were consistent with visual examination of Figure 3 which shows a better fit of the 3D curve at the lower gamma energy. The mathematical model can be easily implemented in any spreadsheet  to generate absolute efficiency values based on gamma energy and soil density.

1. Canberra, Model S574 LabSOCS*™ Calibration Software. 2013) 10.

2. Ortec. Advanced Efficiency Calibration Software for High Purity Germanium Gamma-Ray Detectors. 2012 [cited 2012 October 12]; 8]. Available from: .

   View Article           

3. K. Abbas, F. Simonelli, F. D'Alberti, M. Forte, and M.F. Stroosnijder, Reliability of two calculation codes for efficiency calibrations of HPGe detectors. Applied Radiation and Isotopes. 56. (2002) 703-709. 00269-X

   View Article           

4. M.I. Abbas, HPGe detector photopeak efficiency calculation including self-absorption and coincidence corrections for Marinelli beaker sources using compact analytical expressions. Applied Radiation and Isotopes. 54.(2001) 761-768. 00308-0

   View Article           

5. C. Agarwal, S. Chaudhury, A. Goswami, and M. Gathibandhe, Full energy peak efficiency calibration of HPGe detector for point and extended sources using Monte Carlo code. Journal of Radioanalytical and Nuclear Chemistry. 287.(2011) 701-708.

   View Article           

6. A.S. Ahmed, K. Capello, A. Chiang, E. Cardenas-Mendez, and G.H. Kramer, Optimization of geometric parameters for Marinelli beaker to maximize the detection efficiency of an HPGe detector. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 610.(2009) 718-723.

   View Article           

7. A. Aksoy, Efficiency Inter-Comparison Measurements of Medium and Large Volume HPGe Detectors in Far and Close Geometries. Arabian Journal for Science and Engineering. 36.(2011) 131-136.

   View Article           

8. N. Celik and U. Cevik, Monte Carlo determination of water concentration effect on gamma-ray detection efficiency in soil samples. Applied Radiation and Isotopes. 68.(2010) 1150-1153. PMid:20133141

   View Article      PubMed/NCBI     

9. T.C. Feng, J.P. Cheng, M.Y. Jia, R. Wu, Y.J. Feng, C.Y. Su, and W. Chen, Relationship between Soil bulk density and PVR of In situ Gamma Spectra. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 608.(2009) 92-98.

   View Article           

10. N.Q. Huy, D.Q. Binh, V.X. An, T.T.H. Loan, and N.T. Can, Self-absorption Correction in Determining the 238U activity of Soil samples via 63.keV Gamma ray using MCNP5 code. Applied Radiation and Isotopes. 71.(2013) 11-20. PMid:23079486

    View Article      PubMed/NCBI     

11. J.F. Cameron and M.S. Bourne, A gamma-scattering soil density gauge for subsurface measurements. The International Journal of Applied Radiation and Isotopes. 3.(1958) 15-16, IN11, IN12, 17-19.

12. A.V. de Groot, E.R. van der Graaf, R.J. de Meijer, and M. Maucec, Sensitivity of In-situ Gamma ray Spectra to Soil Density and Water content. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 600. (2009) 519-523.

    View Article           

13. F.L. Melquiades and C.R. Appoloni, Self-absorption Correction for Gamma Spectrometry of Powdered Milk samples using Marinelli beaker. Applied Radiation and Isotopes. 55.(2001) 697-700. 00114-2

    View Article           

14. K. Jackman and S. Biegalski, Methods and software for predicting germanium detector absolute full-energy peak efficiencies. Journal of Radioanalytical and Nuclear Chemistry. 279.(2009) 355-360.

    View Article           

15. K. Jackman, R. Gritzo, and S. Biegalski, A software package using a mesh-grid method for simulating HPGe detector efficiencies. Journal of Radioanalytical and Nuclear Chemistry. 282.(2009) 223-226.

    View Article           

16. Canberra. Model 8715 Analog-to-Digital Converter. 2012 [cited 2012 August 15]; Available from: .

    View Article           

17. C. Tsabaris, G. Eleftheriou, V. Kapsimalis, C. Anagnostou, R. Vlastou, C. Durmishi, M. Kedhi, and C.A. Kalfas, Radioactivity levels of recent sediments in the Butrint Lagoon and the adjacent coast of Albania. Applied Radiation and Isotopes2006) 9.