Jean-claude PEREZ
Email : jeanclaudeperez2@gmail.com jeanclaudeperez3@free.fr
Symmetry and Asymmetry in the MENDELEEV’s Periodic Table Predictive EQUATION
Corresponding Author
Affiliation
Citation
perez, Symmetry and Asymmetry in the MENDELEEV
Abstract
This article demonstrates that: -1- Structure of the periodic table of Elements is predictable. It is structured by a numerical structure of whole numbers. -2- This structure is deterministic and predictive, then, for any period p, it can be calculated by applying "the generic equation of Mendeleev" which we discovered. -3- The generic equation is completely controlled by the four quantum Numbers. -4- This generic equation makes it possible to check the regularity of the common table of Mendeleev, but it can also "predict" and anticipate the existence of hypothetical Elements now unknown, of which it makes it possible to determine the quantum properties, then electronic and chemical hypothetical properties.
Introduction
Let us take the example of the famous table of Mendeleev (1), no one never had the idea to seek a possible mathematical law which would organize the information and the structure of "the most heterogeneous table of Science".
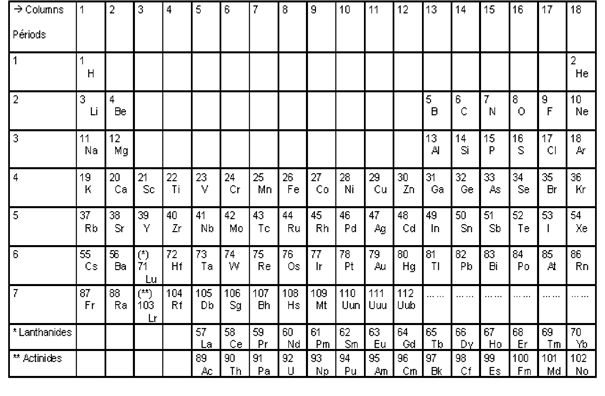
Figure 1 – the conventional representation of the Mendeleev's periodic table.
Figure 2 – the new representation of the Mendeleev's periodic table.
See Figures & tables below
Results
We discovered this law: the equation of the table of Mendeleev. Here is a short summary: We discovered a simple equation which generates and predicts the structure of the table of Mendeleev. This equation predicts the number of elements of any layer of period "p" in the table according to the only value of this period "p".
Beyond this mathematical modelling of the periodic table of the Elements,
- This equation underlines, in its formulation, the " trace" of the 4 fundamental quantum Numbers (please see Methods for details).
-This modelling predicts the structure of the hypothetical extensions of the table of Mendeleev towards possible Elements (real) unknown which would be located beyond the last known radioactive Elements (2).
- This modelling also makes it possible to imagine an infinity of other Elements (virtual ) which one could however predict positioning towards the " low layers of the table ", like their quantum properties.
Summarizing the Law: we consider:
-c(p) a horizontal layer of elements of the table of Mendeleev,
- "p" the period associated with this c(p) layer such as p = [ 1 2 3 4 5 6 7 … ], - Int(v) the whole part of the numerical value "v". exp: if v=2.35, then Int (2.35)=2. one obtains c(p), the number of elements contained in the c(p) layer of order p, by applying the formula:
c(p)□2x□□□Int□□□□p2□2□□□□□□□ 2
Examples :
If p=1 ->c(1)=2
If p=2 -> c(2)=8 If p=3 è c(3)=8
If p=4 -> c(4)=18 If p=5 è c(5)=18
If p=6 -> c(6)=32 If p=7 è c(7)=32
If p=8 -> c(8)=50 If p=9 è c(9)=50 …/… If p=16 -> c(16)=162
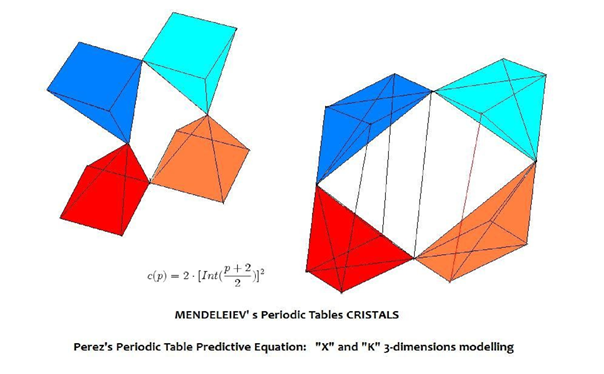
Figure 3 – Perez's periodic table predictive formula: “X” and “K” 3D modelling.
This equation makes it possible to propose new graphic designs of the Mendeleev’s table (3): -« 2-dimensions conventional table » : it is the usual representation in which lanthanides were reintegrated in their place. This table extends by bottom when p increases (please see supplementary information).
-« 3-dimensions X diamonds-like » : this structure underlines the double symmetry of growth of the crystal-like table. It is made of 4 regular pyramids with square bases forming "XX" for face view, "X" for side view, and 2 squares adjacent by an angle in sights of top and below. When p grows, the extension is done alternatively by bottom and the top. The 4 pyramids constitute a network of 4 interconnected "diamonds-like"linked by 4 points: the atoms H and He on the one hand, and corners of the 2 squares of the 2 last layers on the other hand. -« 3-dimensions K diamonds-like » : This structure is most realistic: it amalgamates alignments by columns of the traditional table with the 3-dimensional structure. We have 4 orthogonal pyramids with square bases. They are also connected by the 4 points H, He, and the junctions of the 2 corners of the squares corresponding to the 2 last layers p and p-1. The filling of a layer respects alignments of atoms of the preceding layers (as in the table of Mendeleev) while the new positions of atoms of the layer correspond to the growth of the last squares related to the internal squares of layers (new added orbitals). All in all, the structure falls under 2 adjacent parallelepipeds by a edge. This space is hollowed out by a kind of three-dimensional regular rhombus.
Strong Relationships between the 4 Quantum Numbers and Mendeleev’s Table Equation :
Niels Bohr established the relation between the position of each Element in the periodic table and its electronic structure. The chemical properties of each Element are thus COMPLETELY DETERMINED by the distribution of the electrons of this Element. The properties and positioning of these electrons, themselves, are determined by the laws of QUANTUM PHYSICS. It is related to the wave equation of Schrödinger which establishes these distributions of probabilities of energies of the electron. These waves functions name the " orbitals ". Thus, with any electron identifiers are associated: they are the FOUR
QUANTUM NUMBERS.
One successively defines “n”, “l”, “m”, and “s”, the 4 quantum numbers. We show in additional WEB supplementary information that our Mendeleev’s Equation includes strong links with the 4 quantum numbers: One thus finds, in this new concise writing of the generic equation, the explicit trace of 2 among the 4 quantum Numbers: "n" and "m": c(p)□2x□□□Int□□□□p2 □2□□□□□□□2 = 2mn p = 2nn 2p where m and n are the magnetic and principal quantum numbers of index p.
Symmetry and asymmetry considerations:
Number “2” is generally considered as a key of SYMMETRY. Then, in the proposed single formula, number 2 occurs 4 (four) times: multiply, divide, add, and square power. See details:
- p=1 -> 2 x (1x1) = 2 x 1² = 2 x 1 = 2
- p=2 -> 2 x (2x2) = 2 x 2² = 2 x 4 = 8
- p=3 -> 2 x (2x2) = 2 x 2² = 2 x 4 = 8
- p=4 -> 2 x (3x3) = 2 x 3² = 2 x 9 = 18
- p=5 -> 2 x (3x3) = 2 x 3² = 2 x 9 = 18
- p=6 -> 2 x (4x4) = 2 x 4² = 2 x 16 = 32
- p=7 -> 2 x (4x4) = 2 x 4² = 2 x 16 = 32
- p=8 -> 2 x (5x5) = 2 x 5² = 2 x 25 = 50
- p=9 -> 2 x (5x5) = 2 x 5² = 2 x 25 = 50
- p=10 -> 2 x (6x6) = 2 x 6² = 2 x 36 = 72
- p=11 -> 2 x (6x6) = 2 x 6² = 2 x 36 = 72
In other hand, ASYMETRY appears also within the formula principally in the “Int” operator truncating real numbers in integer numbers and also with alternate odd/even values of period “p”. We note also the great concision of this formula which is build only from 3 tokens: “p”, “2” and “Int” operator. (combined with usual arithmetic basic operators).
Conclusion
- Structure of the periodic table of Elements is predictable. It is structured by a numerical structure of whole numbers.
- This structure is deterministic and predictive, then, for any period p, it can be calculated by applying "the generic equation of Mendeleev" which we discovered.
- The generic equation is completely controlled by the four quantum Numbers.
- This generic equation makes it possible to check the regularity of the common table of Mendeleïev, but it can also "predict" and anticipate the existence of hypothetical Elements now unknown, of which it makes it possible to determine the quantum properties, then electronic and chemical hypothetical properties (4, 5).
Acknowledgement
We especially thank Dr. Robert Friedman M.D. practiced nutritional and preventive medicine in Santa Fe, New Mexico, for strong discussions and suggestions on Mendeleiev's periodic table representations.
Images and Tables
References
Mendeleev D, (1889) The Periodic Law of the Chemical Elements. Journal of the Chemical Society, 55, 634-56 (FARADAY LECTURE , delivered before the Fellows of the Chemical Society in the Theatre of the Royal Institution, on Tuesday, June 4th, 1889) Available: . fr/sitedechimie/hist_chi/text_origin/mendeleiev/mendel.htm
View ArticleGlenn T. Seaborg, "Prospects for further considerable extension of the periodic table", Journal Chemical Education, 1969, 46, 626.
View ArticleMartin Kemp - "Mendele?ev's matrix", NATURE,vol 393, 11 June 1998, p:527, (1998).
Perez JC (2009) Codex Biogenesis. Resurgence, Liege Belgium.
View ArticlePerez JC (1991)HYPERLINK "mailto: " \t "_blank" Chaos DNA and neuro-computers: a golden link. Speculations in Science and Technology 14: 336-346.
View ArticleMarcer PJ (1992)HYPERLINK "mailto: " \t "_blank" Order and chaos in DNA ? the Denis Guichard Prizewinner: Jean-Claude Perez. Kybernetes 21: 60-61. https://doi.org/10.1108/eb005922
View ArticlePerez JC (1997)HYPERLINK "mailto: " \t "_blank" L'adn D?crypt?. Resurgence publisher Liege, Belgium.
View ArticlePerez J (2015) Deciphering Hidden DNA Meta-Codes -The Great Unification & Master Code of Biology. J Glycomics Lipidomics 5:131. doi: 10.4172/2153-0637.1000131 HYPERLINK
View Article