Evgeny V. Tretyakov
Email: tretyakov@nioch.nsc.ru
© 2019 Sift Desk Journals. All Rights Reserved
VOLUME: 2 ISSUE: 2
Page No: 172-178
Evgeny V. Tretyakov
Email: tretyakov@nioch.nsc.ru
Maria M. Petrova,a Svetlana I. Zhivetyeva,b Evgeny V. Tretyakovb*
a Kazan National Research Technological University, 68 K. Marx Str., Kazan 420015, Russia
b N. N. Vorozhtsov Institute of Organic Chemistry, 9 Ac. Lavrentiev Avenue, Novosibirsk 630090, Russia. Fax: +7 383 330 9752.
Arup Kumar Pathak(akpathak@barc.gov.in)
Ju Xie(xieju@yzu.edu.cn)
Lin-Yan Feng(hj.zhai@sxu.edu.cn)
Gabriela L Borosky(gborosky@fcq.unc.edu.ar)
EVGENY TRETYAKOV, Triplet diradicals derived from quinone-nitroxides: a quantum-chemical study(2018)SDRP Journal of Computational Chemistry & Molecular Modelling 2(2)
Quantum-chemical analysis of fluorinated benzo- and naphthoquinones bearing nitronyl nitroxide function revealed that they upon one-electron reduction give triplet diradicals with the large gap of the triplet-singlet splitting (2J ≥ 430 cm-1) that comes from the non-disjoint nature of these diradicals. It was shown that the triplet-singlet splitting is highly sensitive to the number and arrangement of fluorine atoms in the quinone core. Therefore, it is aimed reasonable to synthesize the proposed triplet diradicals and to study the inherent magneto-structural correlations. It is a new synthetic challenge in the field of molecular magnetism.
Keywords: Molecular Magnetism, Nitronyl Nitroxides, Quantum Chemistry Calculations, Quinones, Triplet Diradicals.
The design of ferromagnets based on purely organic compounds is one of major challenges in the field of molecular-based magnets [1]. An important step toward realizing ferromagnetism in organic systems is the development of novel high-spin organic molecules [2] with their subsequent thorough characterization [3]. In our research [4], we have noticed that in the whole family of organic diradicals, there is only one example of a triplet diradical, DR, which is obtained by reduction of a quinone-nitroxide, namely 2,5-dioxocyclohexa-1,4-dienyl-substituted nitronyl nitroxide 1 (Scheme 1) [5].
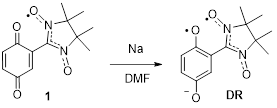
Scheme 1. Preparation of triplet diradical DR from quinone-nitroxide 1.
Considering quinone-nitroxide 1 as a prototype, it was reasonable to determine what compounds of this class would be useful to synthesize. To ensure higher stability of the reduced diradical form DR, two factors could be taken into account: introduction of electron-withdrawing substituents into the quinone core, for example fluorine atoms, or annulation of this core to carbo- or heterocycles.
In this study, we took advantage of quantum-chemical tools to predict the oxidizing ability of various fluorinated quinone-nitroxides, its dependence on the degree of fluorination and the positions of fluorine substituents as well as the sign and energy of the magnetic interaction in the resulting diradicals. Using this strategy, we suggested promising compounds for synthesis.
Computational details
Calculations reported in this paper were performed using spin-unrestricted density functional theory (DFT). Full geometry optimizations of the radical (neutral, N) and diradical (anionic, A) species were carried out within the framework of various computational procedures by means of the ORCA software package (version 3) [6]. In particular, the B3LYP and M06 exchange-correlation functionals were employed in conjunction with the 6-31+G(d,p) basis set. The D3 approach together with Becke–Johnson damping was used to examine the influence of London dispersion interactions (B3LYP-D3/6-31+G(d,p)). A larger basis set was also employed to examine the effect of an increase in basis set size (B3LYP/6-311+G(3df)). In all cases, solvation effects were taken into account via the COSMO solvation model [7] with ε = 36.6 (acetonitrile).
Electron affinities (vertical and adiabatic: EAv and EAad, repsectively) were computed according to the expressions
EAv = Etot(A) – Etot (Neq)
EAad = Etot (Aeq) + ZPE (Aeq) – Etot (Neq) – ZPE (Neq)
where Etot(A) is the diradical total energy calculated at the geometry optimized for the parent radical species, Etot(Neq) and Etot(Aeq) are the radical and diradical total energies computed at their equilibrium geometries, and ZPE(Neq) and ZPE(Aeq) are the corresponding zero point energy corrections.
For diradicals, isotropic exchange parameter JAB was calculated by the broken-symmetry methodology. The scheme proposed by Yamaguchi and coworkers was chosen [8]:
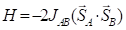
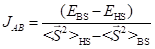
The B3LYP/6-311+G(d,p)//B3LYP/6-31+G(d,p) computational procedure was carried out to compute total energies of the high-spin and broken-symmetry states as implemented in the GAUSSIAN09 package [9]. For all states, stability analysis of the obtained solution was performed.
The B3LYP functional has been successfully applied and well-proved itself in estimating both the electron affinities [10] and the isotropic exchange parameters [11].
A quantum-chemical screening was conducted within a wide range of fluorinated quinone-nitroxides, which can be grouped into three series presented in Figure 1. Within each series, species with different numbers of fluorine substituents and their all possible positions were examined. Their optimized structures and corresponding symbolic labels are given in Figures 2 and 3 for series I and II, respectively. For series III, a similar notation was adopted. We used electron affinities (vertical and adiabatic) as a measure of electron acceptor properties. Their computed values are presented in Tables 1 (for series I) and 2 (for series II and III).
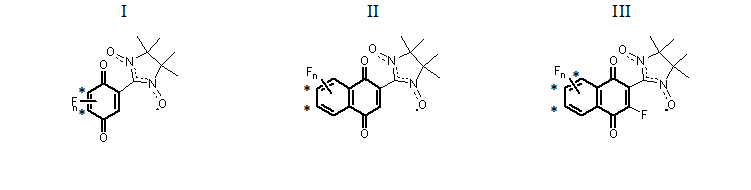
Figure 1. Three series of fluorinated quinone-nitroxides. Positions of fluorine substituents, which provide more negative EA values, are marked by an asterisk.
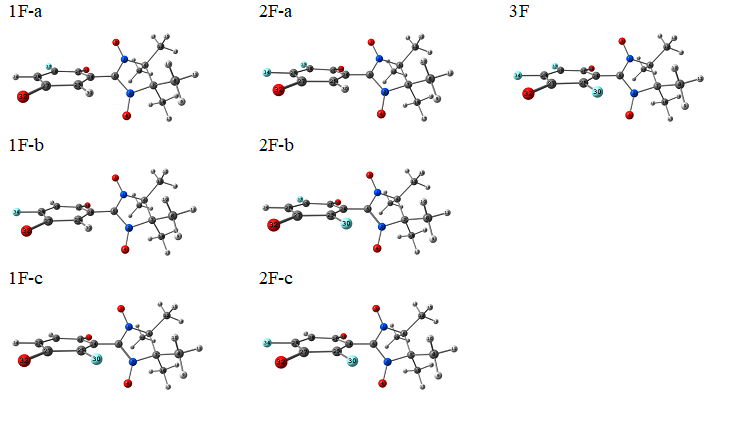
Figure 2. Compounds within series I.
Table 1. Computed values of EA (in eV) for compounds within series I. The EAad values are given without and with (in parentheses) ZPE corrections. nF is the number of fluorine substituents.
|
|
|
B3LYP/6-31+G(d,p) |
M06/6-31+G(d,p) |
B3LYP/6-311+G(3df) |
|||
|
nF |
|
EAv |
EAad |
EAv |
EAad |
EAv |
EAad |
|
1 |
1F-а |
–4.15 |
–4.43 (–4.46) |
–4.18 |
–4.49 |
–4.06 |
–4.37 |
|
|
1F-b |
–4.17 |
–4.44 (–4.47) |
–4.19 |
–4.51 |
–4.10 |
–4.39 |
|
|
1F-c |
–4.13 |
–4.41 (–4.44) |
–4.17 |
–4.48 |
–4.06 |
–4.35 |
|
2 |
2F-а |
–4.30 |
–4.59 (–4.62) |
–4.28 |
–4.64 |
–4.21 |
–4.51 |
|
|
2F-b |
–4.23 |
–4.53 (–4.57) |
–4.26 |
–4.62 |
–4.14 |
–4.45 |
|
|
2F-c |
–4.28 |
–4.57 (–4.61) |
–4.28 |
–4.64 |
–4.19 |
–4.49 |
|
3 |
3F |
–4.39 |
–4.70 (–4.74) |
–4.37 |
–4.78 |
–4.29 |
–4.60 |
For series I (Figure 2), various computational procedures were tested (Table 1). Procedures B3LYP/6-31+G(d,p) and B3LYP-D3/6-31+G(d,p) yield identical results, i.e., the influence of intramolecular dispersion interactions is negligible. For this reason, the EA values for the D3-containing case are omitted in Table 1. From Table 1, it can be concluded that the electron acceptor properties increase in the following order:
{1F-c < 1F-а < 1F-b} < {2F-b < 2F-c < 2F-a} < {3F}.
It is clear that the higher degree of fluorination provides a stronger oxidizing ability. One can also see that two positions of fluorine substituents (marked in Figure 1) have a greater impact on the oxidizing ability, i.e., cause more negative EA values. Note that these conclusions are supported by the data obtained with different basis sets and exchange-correlation functionals, with or without inclusion of the ZPE corrections.
Table 2. Computed values of EA (in eV) for compounds within series II and III. The EAad values are given without the ZPE corrections. nF is the number of fluorine substituents.
|
|
|
B3LYP/6-31+G(d,p) |
|||
|
|
|
II |
III |
||
|
nF |
|
EAv |
EAad |
EAv |
EAad |
|
1 |
1F-а |
–3.83 |
–4.07 |
–3.93 |
–4.18 |
|
|
1F-b |
–3.85 |
–4.10 |
–3.93 |
–4.19 |
|
|
1F-c |
–3.86 |
–4.10 |
–3.95 |
–4.21 |
|
|
1F-d |
–3.83 |
–4.07 |
–3.91 |
–4.16 |
|
2 |
2F-а |
–3.88 |
–4.13 |
–3.98 |
–4.23 |
|
|
2F-b |
–3.90 |
–4.15 |
–4.01 |
–4.26 |
|
|
2F-c |
–3.86 |
–4.10 |
–3.96 |
–4.20 |
|
|
2F-d |
–3.92 |
–4.16 |
–4.00 |
–4.26 |
|
|
2F-e |
–3.89 |
–4.14 |
–3.97 |
–4.22 |
|
|
2F-f |
–3.89 |
–4.13 |
–3.98 |
–4.24 |
|
3 |
3F-а |
–3.95 |
–4.20 |
–4.05 |
–4.31 |
|
|
3F-b |
–3.91 |
–4.16 |
–4.01 |
–4.25 |
|
|
3F-c |
–3.95 |
–4.20 |
–4.04 |
–4.29 |
|
|
3F-d |
–3.92 |
–4.16 |
–4.03 |
–4.28 |
|
4 |
4F |
–3.97 |
–4.22 |
–4.08 |
–4.33 |
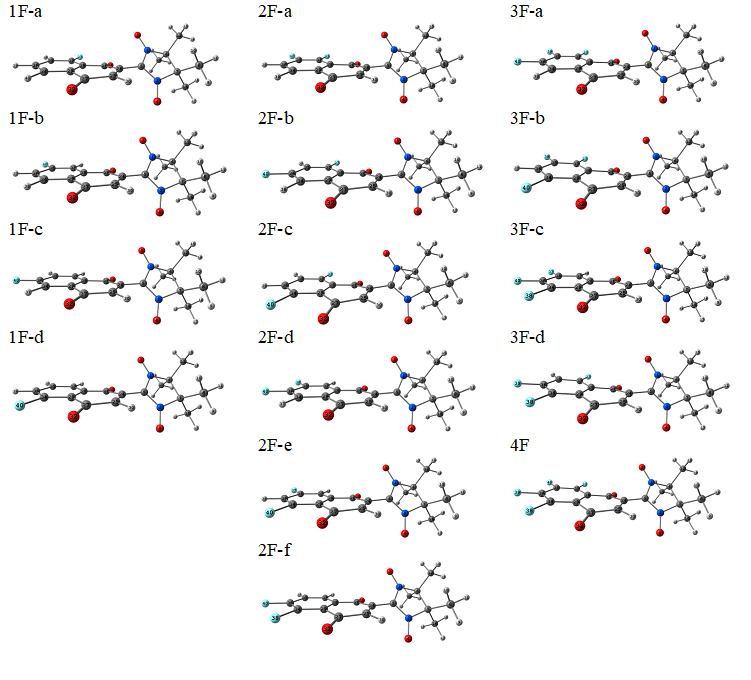
Figure 3. Compounds in series II.
For series II (Figure 3), our computed values of EA are given in Table 2. These data suggest that the oxidizing ability of the compounds within this series increases in the following order:
{1F-a,d < 1F-b,c} < {2F-c < 2F-a,f < 2F-b,e < 2F-d } < {3F-b,d < 3F-a,c} < {4F}.
Again, the oxidizing ability increases with the number of fluorine substituents. Within any given series (nF = 1, 2, or 3), two favorable positions of fluorine substituents can be identified (marked in Figure 1).
The fluorine substituent in the quinone moiety (series III) does not change the above conclusions. Nonetheless, the data in Table 2 suggest that in this case, along with the two previously mentioned positions of fluorine substituents, there is a third position that can also be considered favorable (marked in Figure 1).
In reduced species, the unpaired electrons of quinone and nitroxide moieties are ferromagnetically coupled. In all cases, our computed values of JAB are greater than zero. The energy of isotropic exchange is highly sensitive to structural parameters and is mainly determined by two of them: bond length between the quinone and nitroxide carbon atoms and the dihedral angle between the quinone and nitroxide planes (dCC and φNCCC, respectively). The DFT-computed values of JAB are compiled in Tables 3 (for series I) and 4 (for series II and III), along with the key structural parameters. In Tables 3 and 4, readers can see that shorter dCC and smaller φNCCC provide stronger coupling. The fluorine substituent at the position adjacent to the nitroxide moiety imposes steric constraints, which are reduced by an increase in φNCCC. This situation inevitably leads to weaker coupling (e.g., see data for series II and III). Note that our data were obtained for geometries optimized for a solution in acetonitrile. In the solid phase, intermolecular π–π interactions come into play and induce changes in molecular structure, which will definitely change the energy of intramolecular isotropic exchange.
Table 3. Computed values of JAB (in cm-1) and key structural parameters (dCC in Å and φNCCC in degrees) for compounds within series I.
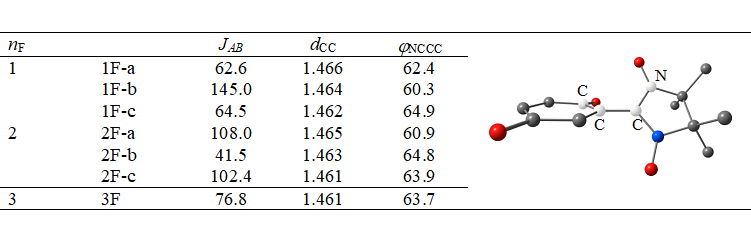
Table 4. Computed values of JAB (in cm-1) and key structural parameters (dCC in Å and φNCCC in degrees) for compounds within series II and III.
|
|
|
II |
III |
||||
|
nF |
|
JAB |
dCC |
jNCCC |
JAB |
dCC |
jNCCC |
|
1 |
1F-а |
196.4 |
1.461 |
58.8 |
142.7 |
1.460 |
63.8 |
|
|
1F-b |
157.6 |
1.462 |
59.1 |
119.2 |
1.461 |
63.6 |
|
|
1F-c |
198.7 |
1.461 |
58.5 |
148.6 |
1.460 |
63.2 |
|
|
1F-d |
137.8 |
1.462 |
59.2 |
101.8 |
1.461 |
63.8 |
|
2 |
2F-а |
173.9 |
1.462 |
59.0 |
127.0 |
1.461 |
63.9 |
|
|
2F-b |
215.0 |
1.461 |
58.4 |
153.8 |
1.460 |
63.6 |
|
|
2F-c |
146.0 |
1.463 |
59.3 |
105.5 |
1.461 |
64.2 |
|
|
2F-d |
174.6 |
1.462 |
58.7 |
129.7 |
1.460 |
63.4 |
|
|
2F-e |
114.2 |
1.463 |
59.4 |
84.1 |
1.461 |
64.0 |
|
|
2F-f |
155.7 |
1.462 |
58.7 |
114.4 |
1.460 |
63.5 |
|
3 |
3F-а |
193.2 |
1.462 |
58.5 |
138.8 |
1.461 |
63.7 |
|
|
3F-b |
122.3 |
1.463 |
59.8 |
89.1 |
1.462 |
64.5 |
|
|
3F-c |
132.5 |
1.463 |
58.9 |
96.6 |
1.461 |
63.8 |
|
|
3F-d |
168.0 |
1.462 |
58.7 |
119.1 |
1.461 |
63.9 |
|
4 |
4F |
146.0 |
1.463 |
59.0 |
104.5 |
1.461 |
64.0 |
Our quantum-chemical analysis of a wide range of fluorinated quinone-nitroxides shows that their oxidizing ability increases with the number of fluorine substituents. Within any given series of species, positions of fluorine substituents having a greater impact on the oxidizing ability were identified. In the resulting diradicals, the unpaired electrons of quinone and nitroxide moieties are expected to be ferromagnetically coupled. The energy of isotropic exchange is highly sensitive to structural parameters, especially to bond length between the quinone and nitroxide carbon atoms and to the dihedral angle between the quinone and nitroxide planes. This finding implies that ferromagnetic coupling may be either enhanced or weakened in the solid phase.
This study revealed polyfluorinated quinone-nitroxides that after one-electron reduction may yield diradicals with a large enough triplet–singlet gap. For synthetic chemists, it is a major challenge to synthesize them and to study the inherent magneto-structural correlations. This is a work in progress.
(a) Supramolecular Engineering of Synthetic Metallic Materials: Conductors and Magnets, (Eds. J. Veciana, C. Rovira, D. B. Amabilino), Kluwer Academic Publishers, Dordrecht/Boston/London, 1999; PMid:10534516 (b) R. G. Hicks, in Stable Radicals: Fundamentals and Applied Aspects of Odd-Electron Compounds, John Wiley and Sons, Chichester, 2010.
View Article PubMed/NCBIP. M. Lahti, in Molecule-Based Magnetic Materials: Theory, Techniques, and Applications, (Eds. M. M. Turnbull, T. Sugimoto, L. K. Thompson), ACS, 1996, Chap. 14, 218–235. PMCid:PMC2143442
(a) D. A. Shultz, in Magnetic Properties of Organic Materials, (Eds. P. M. Lahti, Maecel Dekker), New York, 1999, Chap. 6, 103–125; (b) E. Terada, T. Okamoto, M. Kozaki, M. E. Masaki, D. Shiomi, K. Sato, T. Takui, K. Okada, J. Org. Chem., 2005, 70, 10073–10083. PMid:16292842
View Article PubMed/NCBI(a) M. Haraguchi, E. Tretyakov, N. Gritsan, G. Romanenko, D. Gorbunov, A. Bogomyakov, K. Maryunina, S. Suzuki, M. Kozaki, D. Shiomi, K. Sato, T. Takui, S. Nishihara, K. Inoue, K. Okada, Chem. Asian J., 2017, 12, 2929–2941; View Article PubMed/NCBI (b) E. Tretyakov, A. Keerthi, M. Baumgarten, S. Veber, M. Fedin, D. Gorbunov, I. Shundrina, N. Gritsan, ChemistryOpen, 2017, 6, 642–652; View Article PubMed/NCBI (c) E. Tretyakov, K. Okada, S. Suzuki, M. Baumgarten, G. Romanenko, A. Bogomyakov, V. Ovcharenko, J. Phys. Org. Chem., 2016, 29, 725–734; View Article (d) S. E. Tolstikov, E. V. Tretyakov, D. E. Gorbunov, I. F. Zhurko, M. V. Fedin, G. V. Romanenko, A. S. Bogomyakov, N. P. Gritsan, D. G. Mazhukin, Chem. Eur. J., 2016, 22, 14598–14604; View Article PubMed/NCBI (e) S. Tolstikov, E. Tretyakov, S. Fokin, E. Suturina, G. Romanenko, A. Bogomyakov, D. Stass, A. Maryasov, M. Fedin, N. Gritsan, V. Ovcharenko, Chem. Eur. J., 2014, 20, 2793–2803. View Article PubMed/NCBI
View ArticleR. Kumai, M. Matsushita, A. Izuoka, T. Sugawara, J. Am. Chem. Soc., 1994, 116, 4523–4524.
View ArticleF. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73.
View ArticleS. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen, F. Neese, J. Phys. Chem. A, 2006, 110, 2235. PMid:16466261
View Article PubMed/NCBIM. Shoji, K. Koizumi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura, K. Yamaguchi, Chem. Phys. Lett., 2006, 432, 343.
View ArticleM. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian09, revision A.02, Gaussian, Inc.: Wallingford, CT, 2009.
(a) S. E. Boesch, A. K. Grafton, R. A. Wheeler, J. Phys. Chem., 1996, 100, 10083–10087; View Article (b) A. Modelli, L. Mussoni, D. Fabbri, J. Phys. Chem. A, 2006, 110, 6482–6486. View Article PubMed/NCBI
View Article