Hai Wang
E-mail: wanghai948@126.com
© 2019 Sift Desk Journals. All Rights Reserved
VOLUME: 4 ISSUE: 6
Page No: 804-814
Hai Wang
E-mail: wanghai948@126.com
Zihe Zhanga, Yingna Liua, Xuexia Guob, Shuang Lia, Yu Liub, Guowei Ranb, Jie Wanga, Xinlei Wangc, Hai Wangb,*
a College of Food Science and Technology, Hebei Agricultural University, Hebei, 071000, China
b Chinese Academy of Agricultural Engineering, Beijing, 100125, China
c China Agricultural University, Beijing, 100083, China
Naciye Kutlu Kantar(naciyekutlu@bayburt.edu.tr)
S Reshan Jayawardena(Reshan.JayawardenaMudiyanselage@lincolnuni.ac.nz)
Xiaolin Huang(hxl19880503@163.com)
Yaofeng Zhou(ncuskzhouyaofeng@163.com)
Hai Wang, Zihe Zhang, Yingna Liu, Xuexia Guo, Shuang Li, Yu Liu, Guowei Ran, Jie Wang, Xinlei Wang; Drying characteristics and solar convective drying kinetics of China Hami melon slice (2019)Journal of Food Science & Technology 4(6)
This experimental study aims to investigate the influence of solar drying parameters on water loss of fresh Hami melon flakes. This article presented the experiment results of drying kinetics .In this study, drying kinetics was conducted on a solar convective dryer with heat pump at four air temperatures (i.e., 40 °C, 50 °C, 60 °C, and 70 °C), flow rates (i.e., 1, 2, 3, and 4 m/s), and sample thickness (i.e., 2, 5, 8, and 11 mm). The characteristic drying curve of Hami melon has been determined by experimental results. Eight models were simulated, and the Midilli–Kucuk model had highest fitting degree in thin layer drying models when all drying data was simulated. Within the scope covered, Fick’s second law of diffusion was often used to compute an effective water diffusivity, which raised from 8.66×10−11 m2/s to 3.12×10−9 m2/s with drying temperatures, airflow rates, and thickness. The activation energy is 11.71 kJ/mol, it indicates the effect of temperature on diffusion coefficient.
Keywords: Hami melon; Solar drying; Kinetics; Characteristic drying curve; Drying models
Xinjiang has several distinct climatic characteristics which are advantageous for fostering high-grade sugary and thick-skinned muskmelon. Two hundred years ago, muskmelon was called Hami melon[1]. Hami melon have been seen as an important local characteristic cash crops in Xinjiang where has gross product of 1.1 million tons and planting area of 41,000 ha[2]. They contain numerous health functional constituents, such as ascorbic acid and flavonoids. Simultaneously, high levels of antioxidants are found in Hami melon, and its products aid in preventing oxidative damage that is hazardous for humans. Because of the high temperature in summer, the moisture content of Hami melon was high when it was just harvested. The high temperature and moisture content led to extensive postharvest decay loss up to 20 percent[3]. In addition, low processing rates and backward storage conditions also limit the development of the Hami melon industry.
Drying is a water removal process from wet materials, mainly in order to achieve safe water content[4].This is an old method for preserving agricultural products. In fact, fruits and vegetables ought to be eaten fresh or dried all over the year.
At present, it is open-air drying that the most frequently used method for preserving Hami melon. However, open-air drying depends on an ambient environment. Consequently, drying is time-consuming, and the products can be damaged given insects and microorganisms. Simultaneously, modern industrial drying consumes 10-15% of the world's energy while also increasing carbon dioxide emissions. The use of industrial solar dryers can aid in overcoming the disadvantages of open-air drying, decreasing the consumption of conventional energy, and improving production efficiency[5]. Therefore, solar dryers are regarded as the trend of drying technology innovations in the future.
Numerous studies have been made about the drying characteristics and kinetics of solar drying agricultural products. Koukouch[6] mathematical fitted the solar drying process of raw olive residue. These authors measured the desorption/adsorption equilibrium moisture content of this product is at different drying temperatures (i.e., 30 °C, 40 °C, and 50 °C), and determined LESPAM is the most appropriate model for describing the adsorption of raw olive residue. Mghazli[7] dried Moroccan rosemary leaves in a convection solar dryer and analyzed their drying characteristics and kinetics. These researchers observed that the effective water diffusivity (Deff) varies from 1.48×10−10 to 9.74 × 10−11 in the covered ranges, and the value of activation energy is 54.37 kJ/mol. Moreover, the Midilli–Kucuk model is the best model for depicting the kinetics about rosemary of convective solar drying. Ouaabou[8] presented the convectional drying of two kinds of cherry that applied to a partially indirect solar convective dryer with an area of 2.5 m2. Their results showed that a characteristic drying curve (CDC) suitable for the two kinds of cherry is buit a third-order polynomial in reducing water content. Nasri and Belhamr[9] indicated the impacts of climatic conditions and form on the drying kinetics of potatoes in the Maghreb region. Drying kinetics is subject to the form and size of materiel and analyse the geometrical factors affecting the drying parameters.
However, the moisture evolution in all products cannot be controlled using a single mathematical model[10]. Consequently, the water content and drying rate versus time of diverse drying products must be conducted to determine their drying kinetics. In fact, a single curve called the “CDC” can be used to record all experimental results. The CDC predicts the drying process under various air conditions of the sample.
Eight statistical models (theoretical, empirical, and semi-empirical) were compared in the present study. These mathematical models include Newton, Page, tow-term, Henderson and Pabis, Diffusion approximation, logarithmic, Wang and Singh, Verma, and Midilli–Kucuk. The best model for depicting the solar drying curves of Hami melon and the drying data of this plant were analyzed to get the physical and thermal behavior of viands like effective diffusivity values and activation energy.
So far, we haven't consulted the literature about the solar drying process and kinetics of Hami melon. This work aims to:
2.1. Solar dryer
Tests were carried out using an indirect forced convection solar dryer, which consists of a solar air collector system (SACS), booster heater, air transfer tunnel, drying chamber (DC), and intelligent control center (ICC) (Fig. 1). The solar dryer was fabricated by the Chinese Academy of Agricultural Engineering.
During drying, nine double pass-type solar air heaters with the same size and formation were chained together in series (total 18 m2). This solar air heater also collected solar energy to heat ambient air. Then, the heated air entered the DC lower part the salver and flowed upward past the samples with the function of the fans at a constant velocity to allow water to evaporate from the humid product.
The dimensions of the DC were (1.2 m×2.5 m×1.5 m), with a convection fan (at the bottom) and circulating fan (on the roof). In addition, 10 trays with 0.5 m×1 m surface were arranged with equal spacing in the DC.
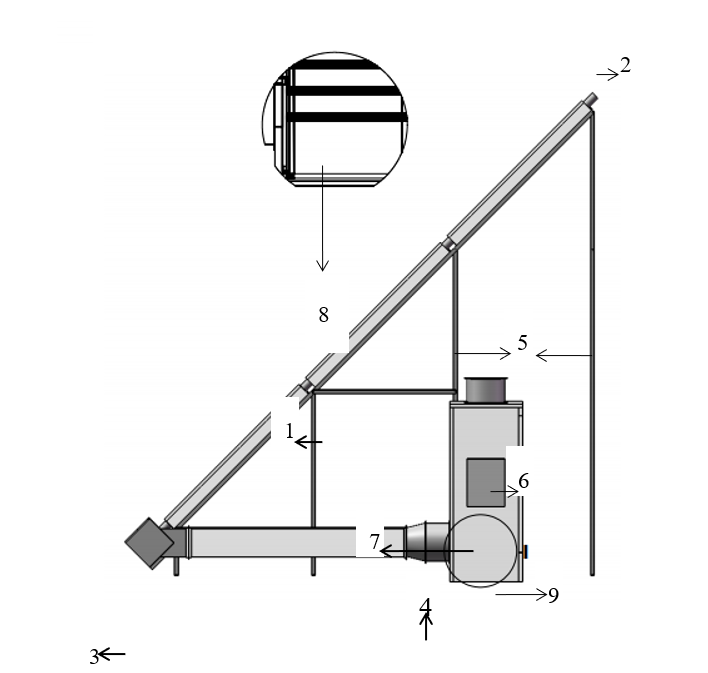
Fig.1. Schematic of a solar dryer. (1) Solar collector; (2) Air inlet; (3) Air transfer tunnel; (4) Convection fan; (5) Trestle; (6) Circulating fan; (7) DC; (8) Tray rack; (9) ICC.
A heat pump was considered an auxiliary heater. The auxiliary heat system compensates a significant drop in temperature when the temperature set by the monitor is higher than the temperature of the solar energy thermal system.
The ICC is the core of the solar dryer to realize the data and automation of the entire drying process. Cr-alumel thermocouples and measurements of relative humidity were conducted by using capacitance transducer, which were placed at the DC and SACS and resulted in inductive changes in the dryer unit. The high-precision indirect forced convection solar dryer might be adjusted to any required drying air temperature from 20 °C to 100 °C and air rate from 0.1 to 5.0 m/s .
We have investigated the drying of Chinese wolfberry, petals, jujubes, and prawns using the solar dryer. In addition, large-scale dryers were used in industrialization in Xinjiang, Ningxia, and other places.
2.2. Drying procedure
Fresh Hami melons were cut into 2, 5, 8, and 11 mm (±0.1 mm) slice thickness with a knife after removing the skin and cockroaches. Hami melon slices used in drying were (500 ± 1) g; the slices were uniformly placed on two drying racks and on the shelf at the bottom of the DC[11]. The drying machine needs to run for at lowest 10 minutes to achieve the set temperature in the DC.
Table 1. Drying condition parameters.
|
test |
drying temperature (°C) |
flow rate (m/s) |
slice thickness (mm) |
|
1 |
70 |
3 |
5 |
|
2 |
60 |
3 |
5 |
|
3 |
50 |
3 |
5 |
|
4 |
40 |
3 |
5 |
|
5 |
60 |
1 |
5 |
|
6 |
60 |
2 |
5 |
|
7 |
60 |
4 |
5 |
|
8 |
60 |
3 |
2 |
|
9 |
60 |
3 |
8 |
|
10 |
60 |
3 |
11 |
All experiments on Hami melon slices were performed through solar drying, as listed in Table 1. For each experiment, environmental conditions were monitored by using a paperless recorder with temperature, humidity, and radiance sensing elements. Dry samples are weighed every hour. Moreover, the second weighing was 5 min more than the first weighing to detect the drying rate until the moisture content is less than 15%. The initial water contents of Hami melon were mensurated by drying them in a bake oven with air aeration of 105 °C for 24 h[12]. The water content and drying rate are expressed as
DR=(M(t+dt)-Mt)/dt (1)
Wb=(Mt-(1-Wb0 ) M0)/Mt (2)
Wb0=(Mt-Mi)/Mt (3)
2.3. Determination of the CDC of Hami melon
Van Meel’s approach showed that the drying kinetics could be depicted by using a functional equation (Eq. 4), and its curve was called the CDC[13]. All drying rate results obtained from 2.2 were single normalized to determine the CDC.
f = f(MR),
MR=(Dbt-Dbeq)/(Db0-Dbeq ) (4)
where MR is the moisture ratio.
Eq. 4 can be reducible to Eq. 5 because the numerical values of Dbeq
Are considerably small compared with those of Dbt or Db0 [14].
MR=Dbt/Db0 (5)
Db has the following relationship with Wb:
Db=Wb/(1-Wb) (6)
Moreover, when constant sample and drying conditions were in a reasonable range, the CDC demonstrates the following characteristics:
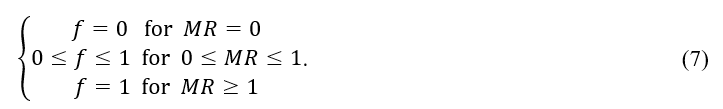
The drying kinetics for Hami melon is determined by using appropriate software (Origin 9, spss22).
2.4. Mathematical modeling for solar drying of Hami melon
Some kinds of empirical or semi-empirical models, which can calculate the moisture content ratio on the basis of time, were used to effectively simulate the drying action. In this study, eight mathematical drying models shown in Table 2 were fitted with the experimental thin layer drying record of Hami melon.
Table 2. Thin layer drying mathematical models.

Three primary statistical quotas were calculated to choose the most suitable model of Hami melon solar drying. The highest coefficient of determination (R2), lowest root of mean square error (RMSE), and reduced chi-square (c2) denote that the model is the most suitable for experimental data[15]. The three parameter values can be expressed as shown below:
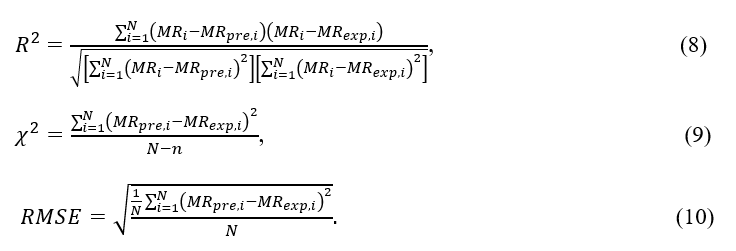
2.5. Effective moisture diffusivity
During the drying process, the Deff is a major parameter used in the mathematical model and for designing and optimizing the drying equipment. According to Fick’s second law of diffusion, the Deff values can be computed and be expressed as follows:

Crank[16] proposed a solution to this equation; this solution can be used for account assumptions, like immobile drying temperature and product size. In this condition, the equation can be simplified to

Eq. 12 is transformed into:

The slope of the straight line of Eq. 13 is set to B, and the Deff can be calculated as follows:

2.6. Activation energy
Dry activation energy is the starting energy needed to measure the removal of a unit mole of water during drying. The Deff correlates with temperature T in accordance with the Arrhenius relationship :

In this equation, is the pre-exponential factor of the Arrhenius equation (m2/s), is the activation energy (), T is the drying temperature (°C), and R is a gas constant, R=8.314 j/ (mol.K).
In Eq. (15), the plot of ln() versus 1/(T+273.15) presents a straight slope of b.
B=Ea/R (16)
The experimental data are used in the equation to gain the coefficient of correlation.
Solar drying tests were conducted between June and September 2018 in Baoding, China. These experiments started at 8:30 and ended in the range of 11:30–20:30. All the ambient conditions are illustrated in Fig. 2, where a, b, and c correspond to temperature, humidity, and irradiance.
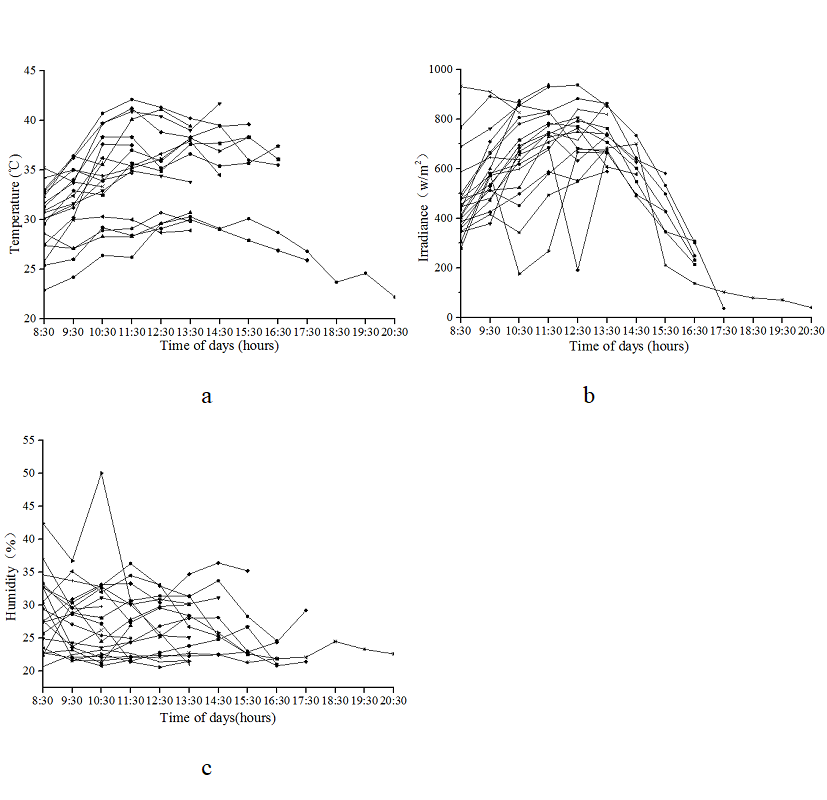
Fig.2. Variations in ambient condition versus time
The external temperatures were obtained between 22.2 °C and 42.1 °C. The environmental humidity varied from 20.6% to 50%, and the solar irradiance varied from 37.7 W/m2 to 937.8 W/m2.
3.1. Drying curves of Hami melon
The relationship between dry base moisture content and drying time under different drying conditions are plotted in Fig.3. The three figures demonstrate the influence of drying temperature, flow rate, and slice thickness on drying when other variables are constant.
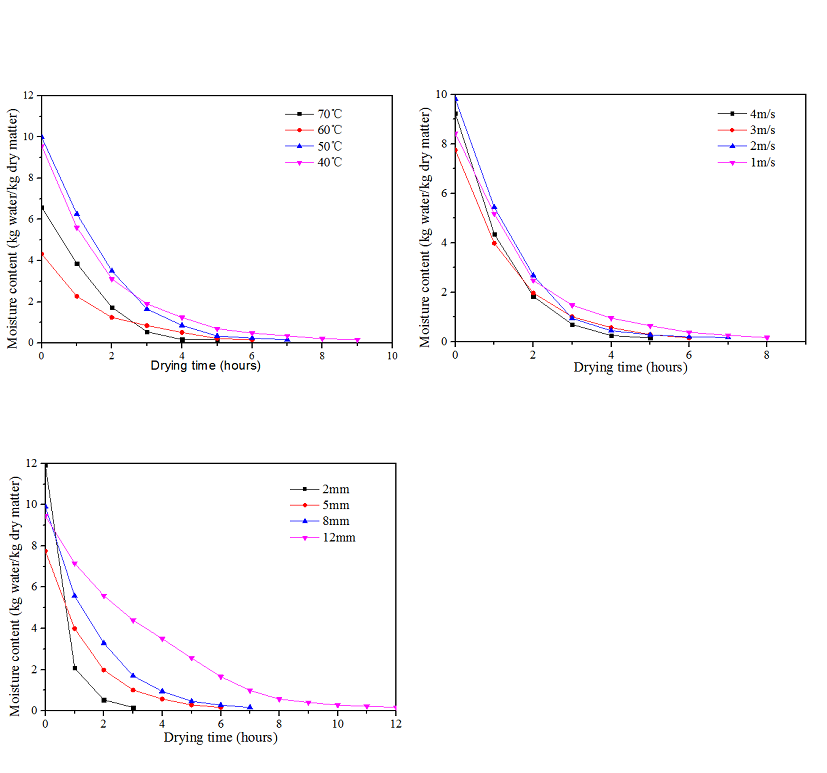
Fig.3 Variation of water content (d.b.) with drying time under different conditions
The dry basis moisture content of Hami melon slices considerably decreases with the increase in drying time for all experiments. In addition, slice thickness, temperature, and flow rate are main elements that influence the drying kinetics of the product. In Fig. 4, thinner thickness, high temperature, and high flow rate as a single variable can significantly increase the drying rate. The findings are consistent with those obtained by several researchers[17-19].
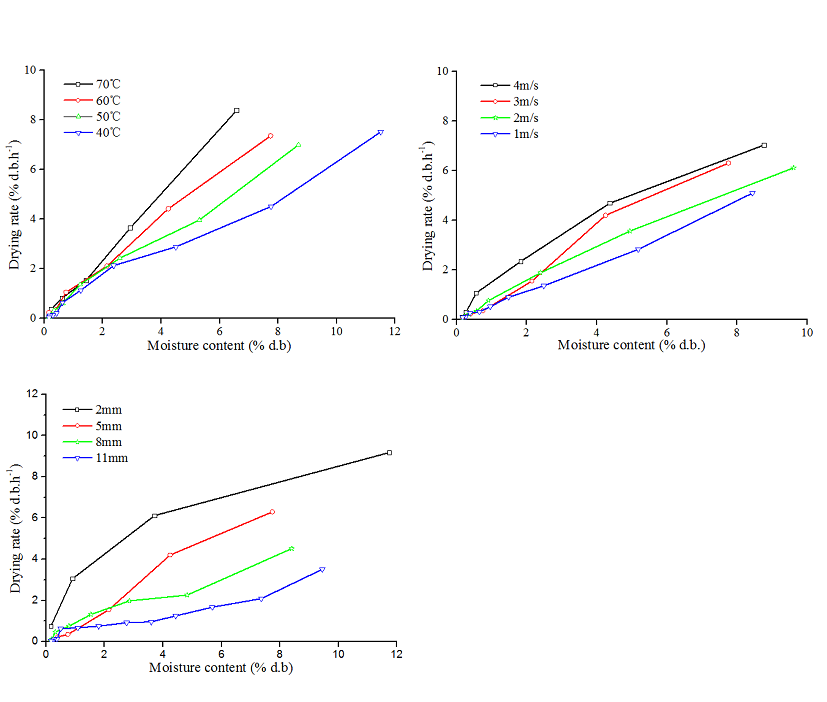
Fig.4 Variation in drying rate with drying time under different conditions
In fact, all drying curves of Hami melon solar drying evidently indicated that only Phase II (speed down stage) exists. The drying rate during this phase hinges on the moisture diffusion activity inside the material. This condition is a complex mechanism, which is generally characterized as an effective water diffusion coefficient and involves various water forms. By contrast, Phases 0 (preliminary stage) and I (constant speed stage) were not reflected during the drying period given the lack of hydrate water at the sample surface.
3.2. CDC of Hami melon
The relation of normalized drying rate and experimental MR is depicted in Fig. 5. We obtained the CDC of Hami melon by using the nonlinear fitting method of Levenberg–Marquardt through Origin 9.0 software. The equation is in the modality of a third-order polynomial.
f = 1.439MR-1.252MR2+ 0.808MR 3
These parameters, such as (RMSE=0.6724) and (R2=0.9748), were used to determine the fineness of the equation.
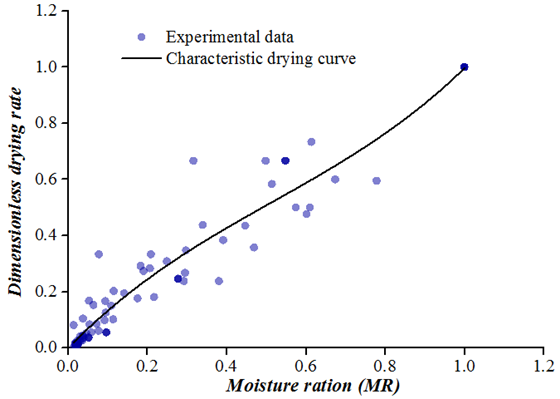
Fig.5. Characteristic drying curve of Hami melon slice
3.3. Modeling of the drying curves
The consequence of nonlinear fitting and regression analysis in the computer program (origin 9.0 and SPSS 22) are listed in Tables 3 and 4. In Table 4, the Midilli–Kucuk model obtains the highest R2 (0.9989) value and lowest values of χ2 (0.0205) and RMSE (0.0008). Therefore, the Midilli–Kucuk model is selected to express the solar drying action for solar drying Hami melon.
Table 3. Statistical consequences of the eight models and their constants and coefficients under different drying conditions
|
Models |
Parameters |
70 °C |
60 °C |
50 °C |
40 °C |
60 °C |
60 °C |
60 °C |
60 °C |
60 °C |
60 °C |
|
5 mm |
5 mm |
5 mm |
5 mm |
5 mm |
5 mm |
5 mm |
2 mm |
8 mm |
1 mm |
||
|
3 m/s |
3 m/s |
3 m/s |
3 m/s |
4 m/s |
2 m/s |
1 m/s |
3 m/s |
3 m/s |
3 m/s |
||
|
Newton |
k |
0.7885 |
0.6715 |
0.5494 |
0.4920 |
0.7940 |
0.6628 |
0.5521 |
2.0741 |
0.5746 |
0.2801 |
|
Logarithmic |
a |
0.9971 |
0.9968 |
1.0484 |
1.0407 |
1.0210 |
1.0236 |
0.9996 |
0.9826 |
1.0085 |
1.0654 |
|
|
k |
0.7915 |
0.6808 |
0.5100 |
0.4780 |
0.7589 |
0.6469 |
0.5765 |
2.2432 |
0.5616 |
0.2396 |
|
|
c |
0.0017 |
0.0038 |
−0.0346 |
−0.0185 |
−0.0178 |
−0.0125 |
0.0117 |
0.0173 |
−0.0085 |
−0.0672 |
|
Wang and Singh |
a |
0.0661 |
0.0475 |
0.0339 |
0.0236 |
0.0665 |
0.0398 |
0.0293 |
0.2244 |
0.0349 |
0.0100 |
|
|
b |
−0.5171 |
−0.4384 |
−0.3711 |
−0.3132 |
−0.5212 |
−0.4090 |
−0.3470 |
−0.9892 |
−0.3765 |
−0.1986 |
|
Diffusion approximation |
a |
0.9998 |
0.6354 |
2.8509 |
1.3955 |
1.5980 |
1.7084 |
0.9984 |
1.0000 |
1.0000 |
1.0000 |
|
|
k |
0.7965 |
0.6719 |
0.8156 |
0.6271 |
0.9830 |
0.8826 |
0.5604 |
2.0741 |
0.5746 |
0.2801 |
|
|
b |
0.9667 |
0.9986 |
1.3184 |
2.7620 |
1.5893 |
1.7633 |
−0.4673 |
1.0000 |
1.0000 |
1.0000 |
|
Midilli–Kucuk |
a |
−0.0009 |
1.0002 |
0.9992 |
1.0000 |
0.9999 |
0.9991 |
1.0033 |
1.0045 |
0.9992 |
0.9897 |
|
|
k |
0.7969 |
0.6712 |
0.4604 |
0.3965 |
0.7497 |
0.5822 |
0.5281 |
2.1310 |
0.5621 |
0.2342 |
|
|
n |
0.9802 |
1.0226 |
1.2321 |
1.2652 |
1.1280 |
1.2373 |
1.1189 |
0.7034 |
1.0179 |
1.0716 |
|
|
b |
0.9669 |
0.0014 |
0.0011 |
0.0018 |
0.0009 |
0.0023 |
0.0037 |
0.0013 |
−0.0006 |
−0.0031 |
|
Page |
k |
0.7969 |
0.6723 |
0.4631 |
0.4018 |
0.7497 |
0.5861 |
0.5365 |
2.1170 |
0.5619 |
0.2301 |
|
|
n |
0.9802 |
0.9982 |
1.2096 |
1.2233 |
1.1131 |
1.1909 |
1.0358 |
0.6631 |
1.0279 |
1.1313 |
|
Verma et al. |
a |
0.9669 |
0.0009 |
2.8509 |
1.3949 |
1.5970 |
1.7079 |
0.0016 |
0.4037 |
1.0198 |
1.0561 |
|
|
k |
0.7664 |
−0.2843 |
0.8156 |
0.6270 |
0.9829 |
0.8826 |
−0.2618 |
1.2106 |
0.5848 |
0.2949 |
|
|
k0 |
0.1750 |
0.6760 |
1.0753 |
1.7338 |
1.5630 |
1.5566 |
0.5604 |
0.7900 |
0.4710 |
1.0222 |
|
Henderson and Pabis |
a |
0.9986 |
1.0004 |
1.0208 |
1.0270 |
1.0056 |
1.0135 |
1.0082 |
0.9997 |
1.0020 |
1.0183 |
|
|
k |
0.7876 |
0.6718 |
0.5591 |
0.5036 |
0.7976 |
0.6702 |
0.5562 |
2.0735 |
0.5757 |
0.2849 |
Table 4. Statistical consequence of the thin layer drying models for solar drying of Hami melon
|
Models |
R2 |
RMSE |
c2 |
|
Newton |
0.9967 |
0.0476 |
0.0032 |
|
Logarithmic |
0.9972 |
0.0399 |
0.0021 |
|
Wang and Singh |
0.9742 |
0.1183 |
0.0177 |
|
Diffusion approximation |
0.9949 |
0.0413 |
0.0034 |
|
Midilli–Kucuk |
0.9989 |
0.0205 |
0.0008 |
|
Page |
0.9987 |
0.0265 |
0.0012 |
|
Verma et al. |
0.9983 |
0.0271 |
0.0015 |
|
Henderson and Pabis |
0.9963 |
0.0497 |
0.0033 |
Fig. 6 exhibits that the predicted MR calculated by the Midilli–Kucuk model and experimental MR are consistent. Fig. 7 presents that the predicted values for MR are almost linear and banded, thus denoting the applicability of the Midilli–Kucuk model during the drying process of Hami melon.
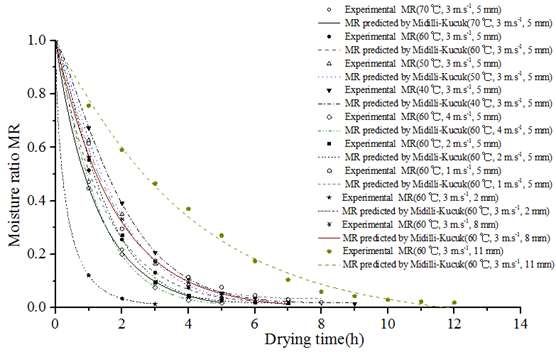
Fig.6. Experimental and predicted MRs versus drying times under different conditions
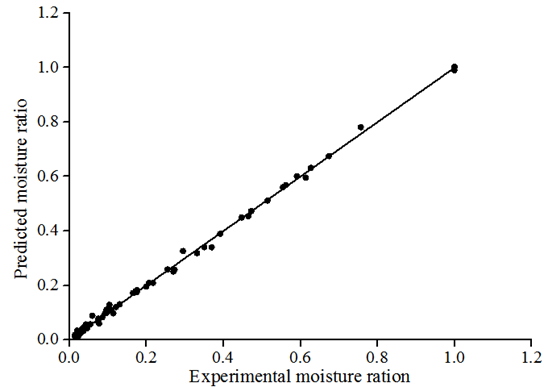
Fig.7. predicted MR using the Midilli–Kucuk model as a function of experimental MR
3.4. Effective moisture diffusivity
Table 5 lists the effective diffusion coefficient values of Hami melon in different conditions, which are calculated on the basis of the relation between ln (MR) and drying time.
The effective moisture diffusivity was found to be dependent on temperature, flow rate, slice thickness, and MR[20]. The effective moisture diffusivity values were positively correlated with drying temperature and flow rate within the appropriate range, such as drying rate. However, this value decreases with the slice thickness. The typical value of agricultural product drying is consistent with the value (10−11–10−8 m2/s) of water diffusivity found in this study[21].
Table 5. Deff of Hami melon slices under different conditions.
|
Test |
T (°C) |
Fr (m.s−1) |
Thickness (mm) |
Deff (m2.s−1) |
R2 |
|
1 |
70 |
3 |
5 |
2.16429×10−09 |
0.99237 |
|
2 |
60 |
3 |
5 |
1.81247×10−09 |
0.99894 |
|
3 |
50 |
3 |
5 |
1.76209×10−09 |
0.98741 |
|
4 |
40 |
3 |
5 |
1.41226×10−09 |
0.97985 |
|
5 |
60 |
1 |
5 |
1.35913×10−09 |
0.99149 |
|
6 |
60 |
2 |
5 |
1.74683×10−09 |
0.95299 |
|
7 |
60 |
4 |
5 |
2.38603×10−09 |
0.99077 |
|
8 |
60 |
3 |
2 |
3.46287×10−10 |
0.94375 |
|
9 |
60 |
3 |
8 |
5.54059×10−09 |
0.99857 |
|
10 |
60 |
3 |
11 |
1.04752×10−08 |
0.97681 |
3.5. Activation energy of solar drying Hami melon slices
Fig. 8 illustrates the values of Ln Deff versus 1/(T+273.15), and Slope B of this straight line is obtained. Moreover, Eq. 16 is used for confirming the activation energy value, as listed in Table 6.
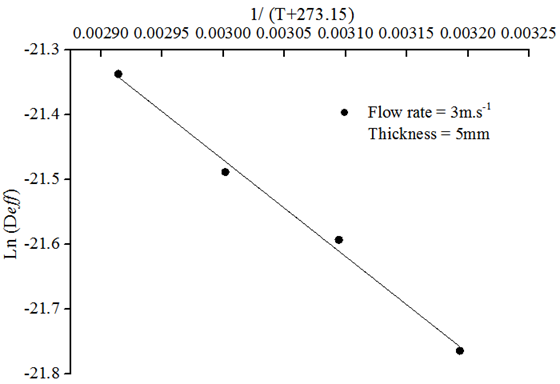
Fig.8. Ln (Deff) versus 1/(T+273.15)
Table 6. Value of the activation energy of Hami melon solar drying and related correlation coefficient.
|
Flow rate (m.s−1) |
3 |
|
Thickness (mm) |
5 |
|
Ea (kJ/mol) |
11.71 |
|
R2 |
0.9017 |
In this study, Hami melon slices were dried successfully using a forced convection solar dryer, and the kinetics analysis of drying the products was performed. We obtained the following conclusions:
Different drying condition parameters (i.e., air temperature, flow rate, and slice thickness) significantly affected drying rates. The drying rate raised with the raise in drying air temperature and flow rate and the decrease in slice thickness.
In this study, the CDC of Hami melon slices were experimentally evaluated to measure the expression of drying rate and establish its correlation.
To describe the drying behavior of Hami melon, eight statistical models were fitted with forced convection solar drying data. Mathematical models were selected by contrasting the correlation ratio and the reduced chi-square and RMSE values. The statistical analysis results showed that the Midilli–Kucuk is the most suitable model.
The effective moisture diffusivity values ranged between 1.04752×10−08 and 1.35913×10−09 and were positively correlated with air temperature, flow rate and slice thickness.
In the covered ranges, the activation energy value obtained from the Arrhenius relation was 11.71 kJ/mol. This value was relatively smaller compared with previous studies.
This research was supported by the Chinese Academy of Agricultural Engineering.
We would also like to thank Hebei Agriculture University for providing experiment place to us.
Nomenclature
|
CDC |
Characteristic drying curve |
|
Deff |
Effective diffusion coefficient |
|
T |
Time |
|
DC |
Drying chamber |
|
SACS |
Solar air collector system |
|
ICC |
Intelligent control center |
|
DR |
Drying rate |
|
MR |
Moisture ratio |
|
f |
Dimensionless drying rate |
|
Wb |
Moisture content |
|
Wb0 |
Initial moisture contentat |
|
Mt |
Sample weight at time (t) |
|
Dbeq |
Equilibrium moisture content |
|
Db0 |
Initial dry basis moisture content |
|
Dbt |
Dry basis moisture content at time (t) |
|
a. k. n. b |
Coefficients of model’s equation |
|
MRexp.i |
Experimental moisture ration |
|
MRpre.i |
Predicted moisture ration |
|
R2 |
Coefficient of determination |
|
T |
Drying temperature (°C) |
|
RMSE |
Root of mean square error |
|
χ2 |
Chisquare |
|
D0 |
Pre-exponential factor of the Arrhenius equation (m2/s) |
| Ea |
Activation energy (kJ/mol) |
|
R |
Gas constant |
Zhang , Y.B., Fan , X.B., Aierken, Y., Ma, X.L., Yi, H.P., Wu, M.Z., 2017. Genetic diversity of melon landraces (Cucumis melo L.) in the Xinjiang Uygur Autonomous Region on the basis of simple sequence repeat markers, Genet. Res. Crop 64, 1023-1035.
View ArticleAierken, Y., Akashi, Y., Phan, T.P.N., Halidan, Y., Tanaka, K., Long, B., Nishida, H., Long, Wu, C.L.M. Z., Kato, K., 2011. Molecular Analysis of the Genetic Diversity of Chinese Hami Melon and Its Relationship to the Melon Germplasm from Central and South Asia, J. Jpn. Soc. Hortic. Sci 80, 52-65.
View ArticleFanta, S.W., Abera, M.K., Aregawi, W.A., 2014. Microscale modeling of coupled water transport and mechanical deformation of fruittissue during dehydration. J. Food Eng. 124, 86-96.
View ArticleBelessiotis, V., Delyannis, E., 2011. Solar drying, Sol. Energy 85, 1665-1691.
View ArticleYuan, G., Hong, L., Li, X., Xu, L., Tang, Wenxue., Wang, Zhifeng., 2015. Experimental investigation of a solar dryer system for drying carpet, Energy Procedia 70, 626-633.
View ArticleKoukouch , A., Idlimam, A., Asbik, M., Sarh, B., Izrar, B., Bah, A., Ansari, O., 2015. Thermophysical characterization and mathematical modeling of convective solar drying of raw olive pomace, Energy Convers. Manag. 99, 221-230.
View ArticleMghazli, S., Ouhammou, M., Hidar, N., Lahnine, L., Idlimam, A., Mahrouz, M., 2017. Drying characteristics and kinetics solar drying of Moroccan rosemary leaves, Renew. Energy 108, 303-310.
View ArticleOuaabou , R., Nabil, B., Hidar, N., Lahnine, L., Idlimam, A., Lamharrar, A., Hanine, H., Mahrouz, M., 2018. Valorization of solar drying process in the production of dried Moroccan sweet cherries, Sol. Energy 172, 158-164.
View ArticleNasris, M.Y., Belhamri, A., 2018. Effects of the climatic conditions and the shape on the drying kinetics, Application to solar drying of potato-case of Maghreb's region, Journal of Cleaner Production 183, 1241-1251.
View ArticleYaldiz, O., Ertekin, C., 2001. Thin layer solar drying of some vegetables, Drying Technology, 19, 583-597.
View ArticleAghbashlo, M., Kianmehr, M.H., Samimi-Akhijahani, H., 2008. Influence of drying conditions on the effective moisture diffusivity, energy of activation and energy consumption during the thin layer drying of berberis fruit (Berberidaceae), Energy Convers. Manage. 49, 2865-2871.
View ArticleHossain, M.A., Woods, J.L., Bala, B.K., 2007. Single-layer drying characteristics and colour kinetics of red chilli, International Journal of Food Science and Technology, 42, 1367-1375.
View ArticleVan Meel, D.A., 1958. Adiabatic convection batch drying with recirculation of air, Chem. Eng. Sci. 9, 36-44. 87005-0
View ArticleDhanushkodia, S., Wilsonb, V.H., Sudhakar, K., 2017. Mathematical modeling of drying behavior of cashew in a solar biomass hybrid dryer, Resource-Efficient Technologies 8, 359-364.
View ArticleMidilli, A., Kucuk, H., Yapar, Z., 2002. A new model for single-layer drying, Drying Technology, 20, 1503-1513.
View ArticleCrank, J., 1975. The Mathematics of Diffusion, Clarendon press, Oxford. UK,
Ertekin, C., Yaldiz, O., 2004. Drying of eggplant and selection of a suitable thin layer drying model, Journal of Food Engineering, 63, 349-359.
View ArticleRahman, S.N.F.S.A., Wahid, R., Rahman, N.A., 2015. Drying kinetics of nephelium lappaceum (rambutan) in drying oven, Procedia-Soc. Behav. Sci. 195, 2734-2741.
View ArticleIdlimam, A., Kane, A.C.S.E., Koujhila, M., 2007. Single layer drying behaviour of grenade peel in a forced convective solar dryer, Rev. Des. Energies Renouvelables 10 (2),191-203.
Liu, X., Qiu, Z., Wang, L., Cheng, Y., Qu, H., Chen, Y., 2009. Mathematical modeling for thin layer vacuum belt drying of Panax notoginseng extract, Energy Convers. Manag. 50, 928-932.
View ArticleDissa, A.O., Desmorieux, H., Bathiebo, J., Koulidiati, J., 2008. Convective drying characteristics of Amelie mango (Mangifera Indica L. cv. 'Amelie') with correction for shrinkage, J. Food Engineering 88, 429-437.
View Article